„Kinematika - 1.4.7” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le: $\mathbf{v}(t)=A\sin(\omega t)\mathbf{i} + B\sin(\omega t+\varphi)\mathbf{j}$ | + | </noinclude><wlatex># Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le: $\mathbf{v}(t)=A\sin(\omega t)\mathbf{i} + B\sin(\omega t+\varphi)\mathbf{j}$, ahol $A=1 m/s$ , $B=2,5 m/s$ , $\omega=1/s$ és $\varphi=60^{\circ}$. |
| − | + | ||
#: a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a $t=0\,s$ időpontban a test az $\mathbf{r}_{0}=x_{0}\mathbf{i} + y_{0}\mathbf{j}$ koordinátájú pontban tartózkodott, ahol $x_{0}=2m$ és $y_{0}=3m$! | #: a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a $t=0\,s$ időpontban a test az $\mathbf{r}_{0}=x_{0}\mathbf{i} + y_{0}\mathbf{j}$ koordinátájú pontban tartózkodott, ahol $x_{0}=2m$ és $y_{0}=3m$! | ||
#: b) Határozza meg a test gyorsulásvektorát az idő függvényében! | #: b) Határozza meg a test gyorsulásvektorát az idő függvényében! | ||
A lap 2013. augusztus 27., 12:52-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le:
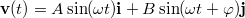, ahol 
, 
, 
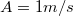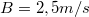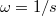és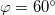 
.
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
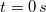időpontban a test az 
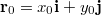koordinátájú pontban tartózkodott, ahol 
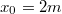és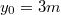 
!
- b) Határozza meg a test gyorsulásvektorát az idő függvényében!
- c) Milyen pályán mozog a test?
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
Megoldás
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.
![\[\mathbf{r}(t)=\mathbf{r}_{0}+\int_{0}^{t}\mathbf{v}(t')dt'=\left(x_{0}-\frac{A}{\omega}\cos(\omega t)\right)\mathbf{i} +\left( y_{0}- \frac{B}{\omega}\cos(\omega t+\varphi)\right)\mathbf{j}\]](/images/math/2/f/4/2f4aef3463c882bca204a2190800fbf0.png)
- b) A gyorsulásvektor
![\[\mathbf{a}(t)=\frac{d\mathbf{v}}{dt}=A\omega\cos(\omega t)\mathbf{i} + B\omega\cos(\omega t+\varphi)\mathbf{j}\,.\]](/images/math/2/d/c/2dca3b96182c5367983d7b411e106adf.png)
- c) A test egy ellipszis pályán mozog.
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.
