„Deriválás - Vektorok felbontása” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Bácsi Ádám {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gya…”)
 
1. sor: 1. sor:
 
<noinclude>
 
<noinclude>
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
−
[[Kategória:Szerkesztő:Bácsi Ádám]]
+
[[Kategória:Szerkesztő: Bácsi Ádám]]
 
{{Kísérleti fizika gyakorlat
 
{{Kísérleti fizika gyakorlat
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
−
| témakör    = Deriválás
+
| témakör    = Integrálás
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex>
+
</noinclude><wlatex># Egy $\alpha$ hajlásszögű lejtőn nyugszik egy $m$ tömegű test.
−
# Adottak az alábbi vektorok.
+
#: a) Határozzuk a gravitációs erő lejtőre merőleges és lejtővel párhuzamos komponenseinek nagyságát!
−
#: $$\mathbf{v}_{1}=\left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]\qquad\qquad\mathbf{v}_{2}=\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]$$
+
#: b) Adjuk meg a nyomóerő függőleges és vízszintes komponenseinek nagyságát!</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $x\sin x+\cos x+C$    b) $e^{2x}\left(\frac{x^{2}}{4}-\frac{x}{2}+\frac{1}{4}\right)+C$   c) $\frac{e^{x}}{2}\left(\sin x-\cos x\right)+C$ }}</wlatex></includeonly><noinclude>
−
#: a) Határozzuk meg az $3\mathbf{v}_{1}-2\mathbf{v}_{2}$ vektort!
+
−
#: b) Mekkora a vektorok normája (nagysága)?
+
−
#: c) Mekkora szöget zár be a két vektor?
+
−
#: d) Adjuk meg a $\mathbf{v}_{1}$ vektor $\mathbf{v}_{2}$ irányába eső komponensét!
+
−
</wlatex>
+
−
<includeonly>
+
−
</includeonly>
+
−
<noinclude>
+
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>
+
<wlatex>#: \begin{itemize}
−
#: a) $$ 3\mathbf{v}_{1}-2\mathbf{v}_{2}= 3 \left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]-
+
\item[a)] A lejt\H ore mer\H oleges komponens nagysága $F_{g1}=mg\cos\alpha$, amely $\alpha=0$ esetben természetesen visszaadja a teljes gravitációs er\H ot.
−
2 \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]= \left[\begin{array}{c} 3 \\ 6 \\ -3 \end{array}\right]-
+
A lejt\H ovel párhuzamos komponens $F_{g2}=mg\sin\alpha$, amely $\alpha=0$ esetben zérus.
−
\left[\begin{array}{c} 0 \\ 2 \\ 2 \end{array}\right]= \left[\begin{array}{c} 3 \\ 4 \\ -5 \end{array}\right]$$
+
\item[b)] A nyomóer\H o a lejt\H ore mer\H oleges irányba mutat úgy, hogy a függ\H olegessel bezárt szöge $\alpha$. Így a függ\H oleges komponensének nagysága $N_{1}=N\cos\alpha$, vízszintes komponnsének nagysága pedig $N_{2}=N\sin\alpha$.</wlatex>
−
#: b) $$|\mathbf{v}_{1}|^{2}=1^{2}+2^{2}+(-1)^{2}=6\qquad\Rightarrow\qquad |\mathbf{v}_{1}|=\sqrt{6}$$$$|\mathbf{v}_{2}|^{2}=0^{2}+1^{2}+1^{2}=2\qquad\Rightarrow\qquad |\mathbf{v}_{2}|=\sqrt{2}$$
+
−
#: c) Bármely két vektor esetén $$\mathbf{v}_{1}\cdot\mathbf{v}_{2}=|\mathbf{v}_{1}||\mathbf{v}_{2}|\cos\alpha\,,$$ ahol $\cdot$ a vektorok skaláris szorzását jelöli és $\alpha$ a két vektor által bezárt szög. Ebben a feladatban $$\mathbf{v}_{1}\cdot\mathbf{v}_{2}=1\cdot 0+ 2\cdot 1+ -1\cdot 1=1\,,$$ tehát $$1=\sqrt{6}\sqrt{2}\cos\alpha\qquad\Rightarrow\qquad \alpha=73,2\,^{\circ}$$
+
−
#: d) A $\mathbf{v}_{2}$ vektor irányába mutató egység vektor $$\mathbf{n}_{2}=\frac{\mathbf{v}_{2}}{|\mathbf{v}_{2}|}=\frac{1}{\sqrt{2}}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.$$ Ezzel az egységvektorral a $\mathbf{v}_{1}$ vektor $\mathbf{n}_{2}$ irányába mutató komponense $$\mathbf{v}_{12}=\mathbf{n}_{2}(\mathbf{n}_{2}\cdot\mathbf{v}_{1})=\frac{1}{2}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.$$
+
−
</wlatex>
+
 
</noinclude>
 
</noinclude>

A lap 2013. április 8., 21:33-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája:
  1. Deriválás
  2. Integrálás
  3. Mozgástan
  4. Erőtan I.
  5. Erőtan II.
  6. Munka, energia
  7. Pontrendszerek
  8. Merev testek I.
  9. Merev testek II.
  10. Rugalmasság, folyadékok
  11. Rezgések I.
  12. Rezgések II.
  13. Hullámok
Integrálás
Feladatok listája:
  1. Alapvető integrálok
  2. Területszámítás
  3. Parciális integrálás
  4. Vegyes integrálok
  5. Tömegközéppont számítás
  6. Időfüggvények
  7. Forgástest
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Egy \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0% hajlásszögű lejtőn nyugszik egy \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegű test.
    a) Határozzuk a gravitációs erő lejtőre merőleges és lejtővel párhuzamos komponenseinek nagyságát!
    b) Adjuk meg a nyomóerő függőleges és vízszintes komponenseinek nagyságát!

Megoldás

  1. \begin{itemize}

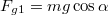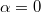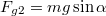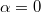\item[a)] A lejt\H ore mer\H oleges komponens nagysága \setbox0\hbox{$F_{g1}=mg\cos\alpha$}% \message{//depth:\the\dp0//}% \box0%, amely \setbox0\hbox{$\alpha=0$}% \message{//depth:\the\dp0//}% \box0% esetben természetesen visszaadja a teljes gravitációs er\H ot. A lejt\H ovel párhuzamos komponens \setbox0\hbox{$F_{g2}=mg\sin\alpha$}% \message{//depth:\the\dp0//}% \box0%, amely \setbox0\hbox{$\alpha=0$}% \message{//depth:\the\dp0//}% \box0% esetben zérus. \item[b)] A nyomóer\H o a lejt\H ore mer\H oleges irányba mutat úgy, hogy a függ\H olegessel bezárt szöge \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%. 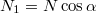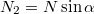Így a függ\H oleges komponensének nagysága \setbox0\hbox{$N_{1}=N\cos\alpha$}% \message{//depth:\the\dp0//}% \box0%, vízszintes komponnsének nagysága pedig \setbox0\hbox{$N_{2}=N\sin\alpha$}% \message{//depth:\the\dp0//}% \box0%.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Deriválás_-_Vektorok_felbontása&oldid=8492”