„Deriválás - Egyszerű deriváltak” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gyakor…”) |
(→Megoldás) |
||
| 20. sor: | 20. sor: | ||
#: d) $$\frac{dh}{dx}=\cos\left[\ln\left(\cos(3x)\right)\right]\cdot\frac{d}{dx}\left[\ln\left(\cos(3x)\right)\right]=\cos\left[\ln\left(\cos(3x)\right)\right]\frac{1}{\cos(3x)}\cdot\frac{d}{dx}\cos(3x)=$$$$=-3\,\mbox{tg}\,(3x)\cos\left[\ln\left(\cos(3x)\right)\right]$$ | #: d) $$\frac{dh}{dx}=\cos\left[\ln\left(\cos(3x)\right)\right]\cdot\frac{d}{dx}\left[\ln\left(\cos(3x)\right)\right]=\cos\left[\ln\left(\cos(3x)\right)\right]\frac{1}{\cos(3x)}\cdot\frac{d}{dx}\cos(3x)=$$$$=-3\,\mbox{tg}\,(3x)\cos\left[\ln\left(\cos(3x)\right)\right]$$ | ||
#: e) $$\frac{dg}{dx}=\frac{e^{\sin x}\cos x+1}{e^{\sin x}+x}$$ | #: e) $$\frac{dg}{dx}=\frac{e^{\sin x}\cos x+1}{e^{\sin x}+x}$$ | ||
| − | #: f) $$\dot{y}=\frac{dy}{dt}=-Ae^{-\lambda t}\left[\lambda\cos(\omega t-\varphi)+\omega\sin(\omega t-\varphi)\right]$$ | + | #: f) $$\dot{y}=\frac{dy}{dt}=-Ae^{-\lambda t}\left[\lambda\cos(\omega t-\varphi)+\omega\sin(\omega t-\varphi)\right]$$$$\ddot{y}=\frac{d^{2}y}{dt^{2}}=Ae^{-\lambda t}\left[(\lambda^{2}-\omega^{2})\cos(\omega t-\varphi)+2\lambda\omega\sin(\omega t-\varphi)\right]$$ Könnyen belátható, hogy $$\ddot{y}+2\lambda\dot{y}+(\omega^{2}+\lambda^{2})y=0\,.$$ |
| − | $$\ddot{y}=\frac{d^{2}y}{dt^{2}}=Ae^{-\lambda t}\left[(\lambda^{2}-\omega^{2})\cos(\omega t-\varphi)+2\lambda\omega\sin(\omega t-\varphi)\right]$$ Könnyen belátható, hogy $$\ddot{y}+2\lambda\dot{y}+(\omega^{2}+\lambda^{2})y=0\,.$$ | + | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. április 8., 22:43-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozzuk meg az alábbi függvények els\H o deriváltját! Az f) feladatrészben a második deriváltat is számoljuk ki!
- a)
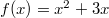
- b)
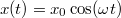
- c)
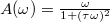
- d)
![\setbox0\hbox{$h(x)=\sin\left[\ln\left(\cos(3x)\right)\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/b/0/1/b011b7760c9d4c61b608cdfbc7c7a95c.png)
- e)
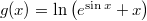
- f)
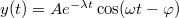
- a)
Megoldás
- a)
![\[\frac{df}{dx}=2x+3\]](/images/math/a/9/0/a90587535e109c295cbbfdfc77fc2a49.png)
- b)
![\[\frac{dx}{dt}=-x_{0}\omega\sin(\omega t)\]](/images/math/b/7/e/b7ed9b6a7ac98072481044da5d91f650.png)
- c)
![\[\frac{dA}{d\omega}=\frac{1+(\tau\omega)^{2}-\omega\cdot 2\tau^{2}\omega}{\left(1+(\tau\omega)^{2}\right)^{2}}=\frac{1-(\tau\omega)^{2}}{\left(1+(\tau\omega)^{2}\right)^{2}}\]](/images/math/5/0/a/50ae158656f8e8a23b7c66237db4d352.png)
- d)
![\[\frac{dh}{dx}=\cos\left[\ln\left(\cos(3x)\right)\right]\cdot\frac{d}{dx}\left[\ln\left(\cos(3x)\right)\right]=\cos\left[\ln\left(\cos(3x)\right)\right]\frac{1}{\cos(3x)}\cdot\frac{d}{dx}\cos(3x)=\]](/images/math/5/a/e/5ae73d8b22ad9076d3b1469507dd3aa5.png)
![\[=-3\,\mbox{tg}\,(3x)\cos\left[\ln\left(\cos(3x)\right)\right]\]](/images/math/0/f/6/0f662af5175c54db3b6bf8a8eaac64a4.png)
- e)
![\[\frac{dg}{dx}=\frac{e^{\sin x}\cos x+1}{e^{\sin x}+x}\]](/images/math/f/3/3/f332db0131328c395ca10eba5ab263fe.png)
- f)
![\[\dot{y}=\frac{dy}{dt}=-Ae^{-\lambda t}\left[\lambda\cos(\omega t-\varphi)+\omega\sin(\omega t-\varphi)\right]\]](/images/math/3/4/8/348b015b90b7b71bc7972bcedec779b3.png) Könnyen belátható, hogy
Könnyen belátható, hogy![\[\ddot{y}=\frac{d^{2}y}{dt^{2}}=Ae^{-\lambda t}\left[(\lambda^{2}-\omega^{2})\cos(\omega t-\varphi)+2\lambda\omega\sin(\omega t-\varphi)\right]\]](/images/math/5/a/5/5a555f745b942123c6fbbd477adcf590.png)
![\[\ddot{y}+2\lambda\dot{y}+(\omega^{2}+\lambda^{2})y=0\,.\]](/images/math/9/3/8/938890a0ca4afe267b7730b2610c24c2.png)
- a)