„Erőtan I. - 2.1.30” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Megrakott $m_{1}=420\,\mathrm{kg}$ tömegű csille $\alpha=8$°-os lejtős pályán lefelé indul. Rakománya $m_{2}=560\,\mathrm{kg}$. A pályán a súrlódási tényező $\mu=0,08$. | + | </noinclude><wlatex># ÁBRAM Megrakott $m_{1}=420\,\mathrm{kg}$ tömegű csille $\alpha=8$°-os lejtős pályán lefelé indul. Rakománya $m_{2}=560\,\mathrm{kg}$. A pályán a súrlódási tényező $\mu=0,08$. |
#: a) Mekkora a gyorsulása? | #: a) Mekkora a gyorsulása? | ||
#: b) Mekkora a sebessége $s_{1}=600\,\mathrm{m}$ út befutása után? | #: b) Mekkora a sebessége $s_{1}=600\,\mathrm{m}$ út befutása után? | ||
A lap 2013. április 22., 17:00-kori változata
Feladat
- ÁBRAM Megrakott
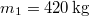tömegű csille 
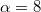°-os lejtős pályán lefelé indul. Rakománya 
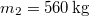. A pályán a súrlódási tényező 
.
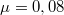- a) Mekkora a gyorsulása?
- b) Mekkora a sebessége
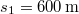út befutása után?
- c) Hány
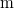hosszú út befutása után kell megkezdeni a fékezést, ha azt akarjuk, hogy a kocsi 
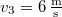-nál jobban ne gyorsuljon fel?
- d) Mekkora fékezőerőt kell alkalmazni a 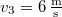állandó sebesség fenntartására?
- e) Mennyi idő alatt fut le a kocsi a lejtőn, ha annak hossza
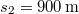, és a 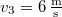elérése után ezzel az állandó sebességgel halad tovább?
Megoldás
- A kocsi és a rakomány a teljes mozgás során együtthalad, ezért csak a közös tömeggel kell számolni:
.
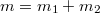- a) A kocsira ható erőket az ÁBRÁn ábrázoltuk. A gravitációs erőt felbontjuk a lejtőre merőleges és lejtővel párhuzamos komponensekre.
- A kocsi és a rakomány a teljes mozgás során együtthalad, ezért csak a közös tömeggel kell számolni:
ÁBRA
A lejtőre merőleges irányban a kocsi nem mozdul el, ezért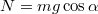
. A lejtővel párhuzamos irányban ![\[ma=F_{g}\sin\alpha-S=mg\sin\alpha-\mu N=mg\left(\sin\alpha-\mu\cos\alpha\right)\]](/images/math/2/f/1/2f16146467e3e520b0e375803edb5bb5.png)
![\[a=g\left(\sin\alpha-\mu\cos\alpha\right)=0,59\,\mathrm{\frac{m}{s^{2}}}\,.\]](/images/math/f/7/f/f7fcd98694a0a9f33d5619cf50a93ddb.png)
- b) Az
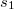utat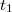 
idő alatt teszi meg, melyre A sebesség az út végén![\[s_{1}=\frac{a}{2}t_{1}^{2}\qquad\Rightarrow\qquad t_{1}=\sqrt{\frac{2s_{1}}{a}}\,.\]](/images/math/2/5/8/2585e2b58b94864629eecbd2b7118362.png)
![\[v_{1}=at_{1}=\sqrt{2s_{1}a}=26,6\,\mathrm{\frac{m}{s}}\,.\]](/images/math/3/b/2/3b220666d2be3d0ebbd587ead7ccbf9d.png)
- c) Ugyanezt az összefüggést használva úton nő a sebesség
![\[s_{3}=\frac{v_{3}^{2}}{2a}=30,5\,\mathrm{m}\]](/images/math/2/7/9/2795993ac08523724a9ca37b8c6a6c8a.png)
.
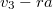- d) Az
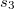út után rögtön el kell kezdeni fékezni, méghozzá fékezőerővel.![\[F=ma=578,2 \,\mathrm{N}\]](/images/math/e/e/2/ee262487f5fa7d3b932841891e5318c2.png)
- e) A fékezésig
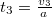idő telik el. A fékezés után egyenletes mozgással még halad a lejtőn. Tehát összesen![\[\Delta t=\frac{s_{2}-s_{3}}{v_{3}}\]](/images/math/3/4/e/34e6a9249cf46f4e466c76f517d267f4.png)
idő alatt fut le a lejtőről.![\[T=t_{3}+\Delta t=\frac{s_{2}}{v_{3}}+\frac{v_{3}}{2a}=155,1\,\mathrm{s}\]](/images/math/c/5/0/c50b32610dc437977e11cf228e184014.png)
- b) Az
