„Erőtan I. - 2.3.1” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Tegyük fel, hogy egy | + | </noinclude><wlatex># (2.3.1) Tegyük fel, hogy egy műhold a földfelszín felett $H=1000 \,\mathrm{km}$ magasságban kering a Föld körül. Mekkora sebességgel keringene, ha csak a Föld vonzóereje hatna rá? |
</wlatex><includeonly><wlatex>{{Végeredmény|content= $v=7348,5\,\mathrm{\frac{m}{s}}$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content= $v=7348,5\,\mathrm{\frac{m}{s}}$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: A | + | <wlatex>#: A műhold pályájának sugara $R=R_{0}+H$, ahol $R_{0}$ a Föld sugara. A műholdra csak a gravitációs erő hat, melynek nagysága $$F=\gamma\frac{mM}{R^{2}}\qquad\qquad \gamma=6,67\cdot 10^{-11}\,\mathrm{\frac{Nm^{2}}{kg^{2}}}\,.$$ A képletben $M$ és $m$ rendre a Föld és a műhold tömege. Ennek az erőnek kell a centripetális erő szerepét játszania (vagy másképpen mondva, a műholddal együtt forgó rendszerben a gravitációs erőnek kell kiegyenlítenie a centrifugális erőt). $$m\frac{v^{2}}{R}=\gamma\frac{mM}{R^{2}}\qquad\Rightarrow\qquad v=\sqrt{\gamma\frac{M}{R}}=\sqrt{\gamma\frac{M}{R_{0}+H}}=7348,5\,\mathrm{\frac{m}{s}}$$ |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. augusztus 27., 18:12-kori változata
Feladat
- (2.3.1) Tegyük fel, hogy egy műhold a földfelszín felett
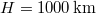magasságban kering a Föld körül. Mekkora sebességgel keringene, ha csak a Föld vonzóereje hatna rá?
Megoldás
- A műhold pályájának sugara
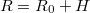, ahol 
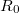a Föld sugara. A műholdra csak a gravitációs erő hat, melynek nagysága A képletben![\[F=\gamma\frac{mM}{R^{2}}\qquad\qquad \gamma=6,67\cdot 10^{-11}\,\mathrm{\frac{Nm^{2}}{kg^{2}}}\,.\]](/images/math/b/0/5/b05f67f651146df5a8f57a9f85aa5f8c.png)
és 
rendre a Föld és a műhold tömege. Ennek az erőnek kell a centripetális erő szerepét játszania (vagy másképpen mondva, a műholddal együtt forgó rendszerben a gravitációs erőnek kell kiegyenlítenie a centrifugális erőt). ![\[m\frac{v^{2}}{R}=\gamma\frac{mM}{R^{2}}\qquad\Rightarrow\qquad v=\sqrt{\gamma\frac{M}{R}}=\sqrt{\gamma\frac{M}{R_{0}+H}}=7348,5\,\mathrm{\frac{m}{s}}\]](/images/math/a/6/e/a6edcf0235891d9ad877a7d387a16601.png)
- A műhold pályájának sugara
