„Kinematika - 1.1.7” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (1.1.7.) Két párhuzamosan haladó sínpáron egy-egy vonat halad egymás felé. Az egyik vonat sebessége $v_{1}=10\,\mathrm{\frac{m}{s}}$, a másiké $v_{2}=20\,\mathrm{\frac{m}{s}}$. A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője $t=1\, \mathrm{s}$ hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség: $c=300\,\mathrm{\frac{m}{s}}$)</wlatex><includeonly><wlatex>{{Végeredmény|content=$$t_{km}=\frac{ | + | </noinclude><wlatex># (1.1.7.) Két párhuzamosan haladó sínpáron egy-egy vonat halad egymás felé. Az egyik vonat sebessége $v_{1}=10\,\mathrm{\frac{m}{s}}$, a másiké $v_{2}=20\,\mathrm{\frac{m}{s}}$. A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője $t=1\, \mathrm{s}$ hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség: $c=300\,\mathrm{\frac{m}{s}}$)</wlatex><includeonly><wlatex>{{Végeredmény|content=$$t_{km}=\frac{28}{30}\,\mathrm{s}$$$$t_{mv}=\frac{28}{31}\,\mathrm{s}$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex># A füttyjel hosszúsága | + | <wlatex># A füttyjel hosszúsága a levegőben $$L=(c-v_{2})t,$$ amennyiben nem fúj a szél. Egy külső, levegőhöz képest álló megfigyelő pontosan annyi ideig hallja a füttyjelet, amíg a hang megteszi az $L$ távolságot, vagyis $$t_{km}=\frac{L}{c}=\frac{c-v_{2}}{c}t=\frac{28}{30}\,\mathrm{s}.$$ A másik vonaton ülő megfigyelő $$t_{mv}=\frac{L}{c+v_{1}}=\frac{c-v_{2}}{c+v_{1}}t=\frac{28}{31}\,\mathrm{s}.$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2013. szeptember 26., 08:25-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (1.1.7.) Két párhuzamosan haladó sínpáron egy-egy vonat halad egymás felé. Az egyik vonat sebessége
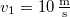, a másiké 
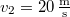. A gyorsabban haladó vonat füttyjelet bocsát ki, melyet a vonat vezetője 
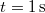hosszúnak észlel. Milyen hosszúnak méri a füttyjelet a töltésen álló, illetve a közeledő vonaton ülő megfigyelő? (hangsebesség: 
)
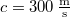Megoldás
- A füttyjel hosszúsága a levegőben amennyiben nem fúj a szél. Egy külső, levegőhöz képest álló megfigyelő pontosan annyi ideig hallja a füttyjelet, amíg a hang megteszi az
![\[L=(c-v_{2})t,\]](/images/math/8/7/9/879d13c2ef9634a467fabdfa4d422bf9.png)
távolságot, vagyis A másik vonaton ülő megfigyelő![\[t_{km}=\frac{L}{c}=\frac{c-v_{2}}{c}t=\frac{28}{30}\,\mathrm{s}.\]](/images/math/9/a/1/9a1a6754eb02dbe8816932a9c3f471c2.png)
![\[t_{mv}=\frac{L}{c+v_{1}}=\frac{c-v_{2}}{c+v_{1}}t=\frac{28}{31}\,\mathrm{s}.\]](/images/math/f/e/9/fe93c6745de8a54ca7f4a5284da6b2bd.png)
