„Kinematika - 1.2.8” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (1.2.8.) Egy motorkerékpáros állandó $v=17 \,\mathrm{\frac{m}{s}}$ sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve $s=400\,\mathrm{m}$ távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor? | + | </noinclude><wlatex># (*1.2.8.) Egy motorkerékpáros állandó $v=17 \,\mathrm{\frac{m}{s}}$ sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve $s=400\,\mathrm{m}$ távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor? |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$T=19,53 \,\mathrm{s}$$$$a=2,1\,\mathrm{\frac{m}{s^{2}}}$$$$v_{max}=41,01\,\mathrm{\frac{m}{s}}$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$T=19,53 \,\mathrm{s}$$$$a=2,1\,\mathrm{\frac{m}{s^{2}}}$$$$v_{max}=41,01\,\mathrm{\frac{m}{s}}$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex># Az észrevétel után a motoros és a rendőr is $s$ utat futott be. A motoros mozgását leíró egyenlet $$s=v(T+\Delta t)$$ alakban írható fel, ahol $T$ az üldözés időtartama és $\Delta t=4\,\mathrm{s}$ a rendőr reakcióideje. Az egyenletből $T$-t kifejezhetjük. $$T=\frac{s}{v}-\Delta t=19,53 \,\mathrm{s}$$ ideig tartott az üldözés. <br> A rendőrre vonatkozó egyenlet $$s=\frac{a}{2}T^{2}\,,$$ ahonnan a rendőr gyorsulása $$a=\frac{2s}{T^{2}}=2,1\,\mathrm{\frac{m}{s^{2}}}$$ <br> Az utolérés pillanatában a rendőr sebessége $$v_{max}=aT=41,01\,\mathrm{\frac{m}{s}}$$ volt. | <wlatex># Az észrevétel után a motoros és a rendőr is $s$ utat futott be. A motoros mozgását leíró egyenlet $$s=v(T+\Delta t)$$ alakban írható fel, ahol $T$ az üldözés időtartama és $\Delta t=4\,\mathrm{s}$ a rendőr reakcióideje. Az egyenletből $T$-t kifejezhetjük. $$T=\frac{s}{v}-\Delta t=19,53 \,\mathrm{s}$$ ideig tartott az üldözés. <br> A rendőrre vonatkozó egyenlet $$s=\frac{a}{2}T^{2}\,,$$ ahonnan a rendőr gyorsulása $$a=\frac{2s}{T^{2}}=2,1\,\mathrm{\frac{m}{s^{2}}}$$ <br> Az utolérés pillanatában a rendőr sebessége $$v_{max}=aT=41,01\,\mathrm{\frac{m}{s}}$$ volt. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 15:15-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*1.2.8.) Egy motorkerékpáros állandó
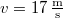sebességgel halad el a rendőr előtt, aki azonnal észreveszi, hogy a motoros bizonyos szabálysértést követett el, és ezért utol kell érnie. Négy másodperccel később a rendőr üldözni kezdi a motorost, állóhelyből indulva, és állandó gyorsulással mozogva. őrhelyétől mérve 
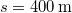távolságban éri utól a motorost. Mennyi időt fordított a rendőr az üldözésre? Mekkora volt a gyorsulása? Mekkora sebességgel haladt a rendőr a motoros beérésekor?
Megoldás
- Az észrevétel után a motoros és a rendőr is
utat futott be. A motoros mozgását leíró egyenlet alakban írható fel, ahol![\[s=v(T+\Delta t)\]](/images/math/6/5/f/65f170046bd70161fa0547930888481c.png)
az üldözés időtartama és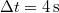 
a rendőr reakcióideje. Az egyenletből -t kifejezhetjük. ideig tartott az üldözés.![\[T=\frac{s}{v}-\Delta t=19,53 \,\mathrm{s}\]](/images/math/3/1/8/318250d04e485d6ace094621e126ba4d.png)
A rendőrre vonatkozó egyenletahonnan a rendőr gyorsulása![\[s=\frac{a}{2}T^{2}\,,\]](/images/math/2/1/3/213bba4632d8b0cff62b37b4902688c0.png)
![\[a=\frac{2s}{T^{2}}=2,1\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/b/f/a/bfa2e5d6a9891f1237618b90d373066b.png)
Az utolérés pillanatában a rendőr sebességevolt.![\[v_{max}=aT=41,01\,\mathrm{\frac{m}{s}}\]](/images/math/5/4/7/5473c39b89f69ddf42c67e5163f56e7f.png)
