„Kinematika - 1.4.7” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (1.4.7) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le: $\mathbf{v}(t)=A\sin(\omega t)\mathbf{i} + B\sin(\omega t+\varphi)\mathbf{j}$. | + | </noinclude><wlatex># (*1.4.7) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le: $\mathbf{v}(t)=A\sin(\omega t)\mathbf{i} + B\sin(\omega t+\varphi)\mathbf{j}$. |
#: a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a $t=0\,s$ időpontban a test az $\mathbf{r}_{0}=x_{0}\mathbf{i} + y_{0}\mathbf{j}$ koordinátájú pontban tartózkodott! | #: a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a $t=0\,s$ időpontban a test az $\mathbf{r}_{0}=x_{0}\mathbf{i} + y_{0}\mathbf{j}$ koordinátájú pontban tartózkodott! | ||
#: b) Határozza meg a test gyorsulásvektorát az idő függvényében! | #: b) Határozza meg a test gyorsulásvektorát az idő függvényében! | ||
A lap 2014. január 9., 16:19-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*1.4.7) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le:
.
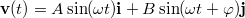- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
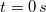időpontban a test az 
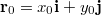koordinátájú pontban tartózkodott!
- b) Határozza meg a test gyorsulásvektorát az idő függvényében!
- c) Milyen pályán mozog a test, ha
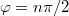valamilyen 
egész számmal?
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
Megoldás
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.
![\[\mathbf{r}(t)=\mathbf{r}_{0}+\int_{0}^{t}\mathbf{v}(t')dt'=\left(x_{0}+\frac{A}{\omega}-\frac{A}{\omega}\cos(\omega t)\right)\mathbf{i} +\left( y_{0}+\frac{B}{\omega}\cos\varphi- \frac{B}{\omega}\cos(\omega t+\varphi)\right)\mathbf{j}\]](/images/math/f/6/2/f62220f95be66aa4732794d4b5e8a0a2.png)
- b) A gyorsulásvektor
![\[\mathbf{a}(t)=\frac{d\mathbf{v}}{dt}=A\omega\cos(\omega t)\mathbf{i} + B\omega\cos(\omega t+\varphi)\mathbf{j}\,.\]](/images/math/2/d/c/2dca3b96182c5367983d7b411e106adf.png)
- c) Vezessük be az
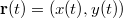helyvektor komponensei helyett az változókat a rövidebb jelölés érdekében! Ez a transzformáció egy eltolásnak felel meg. A helyvektor komponenseinek időfüggése alapján![\[X(t)=x(t)-x_{0}-\frac{A}{\omega}\qquad \mbox{és}\qquad Y(t)=y(t)-y_{0}-\frac{B}{\omega}\cos\varphi\]](/images/math/2/3/c/23c7a9ce7f2bbddb84b64c3501bdeca0.png)
Az egyenletek átrendezhetők olyan formába, amelyben az időfüggést már csak![\[X(t)=-\frac{A}{\omega}\cos(\omega t) \qquad \mbox{és} \qquad Y(t)=-\frac{B}{\omega}\cos(\omega t)\cos\varphi + \sin(\omega t)\sin\varphi\,.\]](/images/math/d/4/f/d4f36b09f8b09e8fce5e188c69e98019.png)
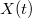és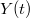 
hordozzák. Ez az egyenlet határozza meg a test pályáját. A feladatban csak a![\[\left(\frac{\omega X(t)}{A}\right)^2-2\left(\frac{\omega X(t)}{A}\right)\left(\frac{\omega Y(t)}{B}\right)\cos\varphi+\left(\frac{\omega Y(t)}{B}\right)^2=\sin^{2}\varphi\]](/images/math/1/8/b/18b0da425bbbf3690da0d67c7813a242.png)
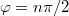eseteket kell vizsgálni, ahol egy egész szám. Ha páros, akkor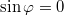 
és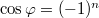 
, vagyis a pálya egyenlete alakban írható. Tovább alakítva![\[X^2-2XY+Y^2=0\qquad\mbox{vagy}\qquad X^2+2XY+Y^2=0\]](/images/math/5/7/e/57e80040ed1e2d816531a6928fdf2ee2.png)
egyenletet kapunk, vagyis a pálya egyenlete egy egyenes menti harmonikus rezgőmozgást ír le.![\[X=Y\qquad\mbox{vagy}\qquad X=-Y\]](/images/math/e/b/5/eb5df0155107a4515dead9818891f7ea.png)
Ha páratlan, akkor 
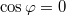és 
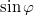a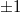 
értékeket veheti fel, mindkét esetben 
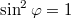. A pálya egyenlete ekkor alakban írható. Amennyiben![\[\left(\frac{\omega X(t)}{A}\right)^2+\left(\frac{\omega Y(t)}{B}\right)^2=1\]](/images/math/a/e/5/ae5f5084f1dcd266ce3b746416a70b99.png)
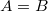, az egyenlet egy körmozgást ír le. Egyéb esetekben a test egy ellipszis pályán mozog.
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.
