Erőtan I. - Harmonikus rezgés gravitációs térben
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Werner (vitalap | szerkesztései) 2014. október 14., 19:38-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan I. |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy
 direkciós erejű rugó egyik végét a plafonhoz rögzítettük, másik végére pedig
direkciós erejű rugó egyik végét a plafonhoz rögzítettük, másik végére pedig  tömegű testet kötöttünk, amihez egy további fonalállal egy másik, szintén
tömegű testet kötöttünk, amihez egy további fonalállal egy másik, szintén  tömegű testet kötöttünk.
tömegű testet kötöttünk.
- a.) Mekkora a rugó megnyúlása egyensúlyi helyzetben?
- b.) Kicsit kitérítve az egyensúlyi helyzetből, mekkora lesz a kialakuló rezgés körfrekvenciája?
- Legyen ismét egyensúlyban a rendszer. Ekkor elvágjuk a fonalat.
- c.) Hol lesz az a rendszer új egyensúlyi helyzete?
- d.) Mekkora lesz az új körfrekvencia?
- e.) Mekkora amplitudójú rezgést végez a megmaradt test?
- f.) Adjuk meg a rezgés kitérés-idő függvényét!
Megoldás
- a.) Mivel a feladat nem kérdezi a fonal-erőt, ezért egyszerűen azt mondhatjuk, hogy a rugóra egy
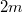 tömegű test van rákötve. Ez mindaddig helyes, amíg a fonal esetleg meg nem lazul. A rugó egyensúlyi megnyúlása
tömegű test van rákötve. Ez mindaddig helyes, amíg a fonal esetleg meg nem lazul. A rugó egyensúlyi megnyúlása ![\[x_{e,0} = \frac{2 m g}{D} \; .\]](/images/math/9/2/d/92d47aefe94ae638fa6cdfefe0d04ea5.png)
- b.) Mindaddig, amíg a fonal feszes marad (nem túl nagy amplitudójú rezgés), tekinthetjük úgy, hogy egy
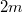 tömegű test mozog. A mozgásegyenlete Érdemes áttérni az
tömegű test mozog. A mozgásegyenlete Érdemes áttérni az![\[ 2m \ddot{x} = 2m g - D x \, .\]](/images/math/1/4/5/145c1727b862622ffe217f9203eed282.png)
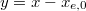 koordinátára. Ezt behelyettesítve Láthatóan egy konstans erővel terhelt harmonikus oszcillátor ismét egy harmonikus oszcillátor, csak az egyensúlyi helyzete eltolódik. A rezgés körfrekvenciája
koordinátára. Ezt behelyettesítve Láthatóan egy konstans erővel terhelt harmonikus oszcillátor ismét egy harmonikus oszcillátor, csak az egyensúlyi helyzete eltolódik. A rezgés körfrekvenciája![\[2 m \ddot{y} = - D y \; .\]](/images/math/f/0/8/f08d7444ec55b15a68de67c6ab5fdf39.png)
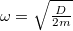 . (Azt, hogy ez hogy jön ki, a d.) feladat megoldása alapján itt is meg lehet csinálni.)
. (Azt, hogy ez hogy jön ki, a d.) feladat megoldása alapján itt is meg lehet csinálni.)
- c.) Levágva az alsó tömeget, az új egyensúlyi helyzet
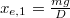 .
.
- d.) Bevezetve a
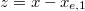 koordinátát a mozgásegyenlet: Ennek az egyenletnek az általános megoldása
koordinátát a mozgásegyenlet: Ennek az egyenletnek az általános megoldása![\[m \ddot{z} = - D z \; .\]](/images/math/d/0/9/d0946869af3a7660a625dd6852227fd0.png) Helyettesítsük be az általános megoldást!
Helyettesítsük be az általános megoldást!![\[z(t) = A \sin (\omega t + \varphi) \, .\]](/images/math/f/e/9/fe93c1dd541a275856bb3b21ed48d574.png) Láthatóan oszthatunk
Láthatóan oszthatunk![\[- m A \omega^2 \sin(\omega t + \varphi) = - D A \sin (\omega t + \varphi) \, .\]](/images/math/7/5/a/75af9823987d50f85a78b76ad25aba23.png)
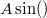 -al, amit kapunk: , ebből
-al, amit kapunk: , ebből![\[m \omega^2 = D\]](/images/math/d/d/e/dded9dda728292c50fdd6db4f460bfda.png)
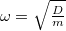 .
.
- e.) Az
 és
és  paramétereket a kezdeti feltételek illesztésével nyerhetjük. A kezdőpillanatban a testünk a régi egyensúlyi helyen volt, azaz
paramétereket a kezdeti feltételek illesztésével nyerhetjük. A kezdőpillanatban a testünk a régi egyensúlyi helyen volt, azaz 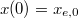 . Ebből a kezdeti
. Ebből a kezdeti  koordináta
koordináta  . A kezdeti sebesség
. A kezdeti sebesség 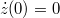 Ezeket az egyenleteket felírva az általános megoldással:
Ezeket az egyenleteket felírva az általános megoldással: ![\[A \sin(\varphi) = z(0) = \frac{m g}{D}\]](/images/math/b/a/d/bad7ab67baa6b2e5390aa6e83e0ebf36.png) A második egyenletből
A második egyenletből![\[A \omega \cos(\varphi) = 0 \; .\]](/images/math/2/6/9/269ea784120bfa90ee9241f20a3bc23d.png)
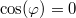 , azaz
, azaz 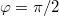 megfelelő. Ezt beírva az elsőbe
megfelelő. Ezt beírva az elsőbe 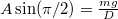 , azaz
, azaz 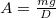 .
.
- f.)
![\[z(t) = \frac{m g}{D} \sin(\omega t + \pi/2) = \frac{m g}{D} \cos(\omega t)\]](/images/math/1/f/0/1f01b2356a7d4323fcdfe60ebf0b7da6.png)
- a.) Mivel a feladat nem kérdezi a fonal-erőt, ezért egyszerűen azt mondhatjuk, hogy a rugóra egy
