Kinematika - 1.4.17
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 22., 15:31-kor történt szerkesztése után volt.
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- ÁBRA Egy gőzgép hajtókereke egyenletes
 szögsebességgel forog az
szögsebességgel forog az  középpontján átmenő tengely körül. A kerék
középpontján átmenő tengely körül. A kerék  hosszúságú hajtórúdjának
hosszúságú hajtórúdjának  csuklópontja az
csuklópontja az  -tól
-tól  távolságban van,
távolságban van,  vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az
vége pedig a dugattyúkarhoz csatlakozik, amely vízszintesen mozog ide-oda. Mekkora az  pont sebessége abban a pillanatban, amikor
pont sebessége abban a pillanatban, amikor 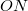 a vízszintessel
a vízszintessel  szöget zár be? (
szöget zár be? ( a dugattyú-karral egy egyenesen fekszik.)
a dugattyú-karral egy egyenesen fekszik.)
Megoldás
- Vegyük kezdőpillanatnak azt, amikor az
 csuklópont az
csuklópont az 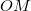 egyenesre illeszkedik, vagyis amikor
egyenesre illeszkedik, vagyis amikor 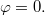 Az
Az  pont elmozdulását a hajtókerék irányába jelöljük
pont elmozdulását a hajtókerék irányába jelöljük 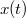 -vel. Az
-vel. Az 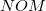 háromszögre cosinus-tételt alkalmazva adódik, ahol
háromszögre cosinus-tételt alkalmazva adódik, ahol![\[(l-r)^{2}=r^{2}+(l-x(t))^{2}-2r(l-x(t))\cos(\varphi(t))\]](/images/math/8/1/1/811aa713e1d69108c5bf93ded26ae2e2.png)
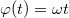 . Az elmozdulást kifejezve az eredményre jutunk, melyek közül a negatív előjeles megoldás lesz fizikai. Az
. Az elmozdulást kifejezve az eredményre jutunk, melyek közül a negatív előjeles megoldás lesz fizikai. Az![\[x(t)=l-r\cos(\omega t)\pm\sqrt{(l-r)^{2}-r^{2}\sin^{2}(\omega t)}\]](/images/math/6/c/5/6c53eaa2f1667f365a16d33c8652c41a.png)
 pont sebessége
pont sebessége ![\[v(t)=\frac{dx}{dt}=r\omega\sin\varphi\left[1+\frac{r\cos\varphi}{\sqrt{(l-r)^{2}-r^{2}\sin^{2}\varphi}}\right]\,.\]](/images/math/6/7/6/6765f20b6e367f380b9be0bbc291a7db.png)
- Vegyük kezdőpillanatnak azt, amikor az