Kinematika - 1.4.18

Feladat

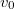1. Egy vékony egyenes cső $\setbox0\hbox{$0$}% \message{//depth:\the\dp0//}% \box0%$ pontja körül állandó $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel forog vízszintes síkban. A csőben egy golyó mozog a csőhöz képest állandó $\setbox0\hbox{$v_{0}$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel. Milyen pályát ír le a golyó a csövön kívül álló megfigyelőhöz képest és mekkora a sebessége, mint az idő függvénye?
   

Megoldás

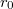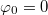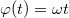1. Tegyük fel, hogy a golyó a $\setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0%$ időpillanatban $\setbox0\hbox{$r_{0}$}% \message{//depth:\the\dp0//}% \box0%$ távolságban van az origótól és cső éppen vízszintes helyzetben, vagyis $\setbox0\hbox{$\varphi_{0}=0$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\varphi(t)=\omega t$}% \message{//depth:\the\dp0//}% \box0%$. A golyó mozgását először polár koordináták segítségével írjuk fel.

   $\[r(t)=|r_{0}-v_{0}t|\qquad\qquad\varphi(t)=\omega t\]$

   Az abszolút értékkel figyelembe vettük azt az esetet is, amikor a golyó már áthaladt az origón. A polár koordináták alapján a Descartes-koordináták a külső megfigyelő rendszerében

   $\[x(t)=r(t)\cos\varphi(t)=|r_{0}-v_{0}t|\cos(\omega t)\]$

   $\[y(t)=r(t)\sin\varphi(t)=|r_{0}-v_{0}t|\sin(\omega t)\,.\]$

A sebesség, mint az idő függvénye, az alábbiak szerint írható fel.

$\[v_{x}(t)=\frac{dx}{dt}=v_{0}\mathrm{sgn}(v_{0}t-r_{0})\cos(\omega t)-\omega|r_{0}-v_{0}t|\sin(\omega t)\]$

$\[v_{y}(t)=\frac{dy}{dt}=\frac{dx}{dt}=v_{0}\mathrm{sgn}(v_{0}t-r_{0})\sin(\omega t)+\omega|r_{0}-v_{0}t|\cos(\omega t)\]$