Deriválás - Hiperbolikus függvények
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 8., 21:53-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- A hiperbolikus függvényeket a következ\H oképpen definiáljuk.
![\[\mbox{ch}\,x=\frac{e^{x}+e^{-x}}{2}\qquad\qquad \mbox{sh}\,x= \frac{e^{x}-e^{-x}}{2}\qquad\qquad \mbox{th}\,x=\frac{\mbox{sh}\, x}{\mbox{ch}\, x}\qquad\qquad \mbox{cth}\,x=\frac{\mbox{ch}\,x}{\mbox{sh}\,x}\]](/images/math/9/e/f/9efca5f7b1f80ce2343bdd76d49f75b6.png)
- a) Igazoljuk, hogy
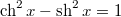 !
!
- b) Számoljuk ki a hiperbolikus függvények deriváltjait!
- c) Határozzuk meg a
 függvény inverzét és annak deriváltját.
függvény inverzét és annak deriváltját.
- a) Igazoljuk, hogy
Megoldás
- a) A hiperbolikus függvények definícióját behelyettesítve az állítás könnyedén igazolható.
- b)
![\[\frac{d}{dx}\mbox{ch}\,x=\frac{e^{x}-e^{-x}}{2}=\mbox{sh}\,x\qquad\qquad \frac{d}{dx}\mbox{sh}\,x=\frac{e^{x}+e^{-x}}{2}=\mbox{ch}\,x\]](/images/math/a/c/f/acf9d2f7931271b4c115b87bb1b03e60.png)
![\[\frac{d}{dx}\mbox{th}\,x=\frac{1}{\mbox{ch}^{2}\,x}\qquad\qquad \frac{d}{dx}\mbox{cth}\,x=-\frac{1}{\mbox{sh}^{2}\,x}\]](/images/math/5/7/0/570b5e1a5336736e574f599f01308042.png)
- c) A
 függvény inverzét
függvény inverzét 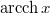 -val jelöljük.
-val jelöljük. ![\[\mbox{arcch}\,x=y(x)\]](/images/math/c/5/1/c51b20f0ea9331b5b3503ec05638768f.png)
![\[x=\mbox{ch}\, y\]](/images/math/e/4/4/e44635f7037bd8ffa9dbab6539501a2e.png)
![\[x=\frac{e^{y}+e^{-y}}{2}\]](/images/math/9/4/5/94566b2f3b643adb5d6d5a73c2e8b56d.png)
![\[e^{2y}-2xe^{y}+1=0\]](/images/math/5/d/6/5d6080e5779c19319074073c7d810dd6.png) A két megoldás közül az egyik
A két megoldás közül az egyik![\[e^{y}=x\pm \sqrt{x^{2}-1}\]](/images/math/5/c/e/5ceae14a29e6f6a70b53b426d31d10b7.png)
 -nak, a másik pedig
-nak, a másik pedig 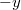 -nak felel meg. Konvencionálisan a
-nak felel meg. Konvencionálisan a 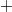 el\H ojelet tekintjük az
el\H ojelet tekintjük az 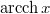 függvényben.
függvényben. ![\[e^{y}=x+ \sqrt{x^{2}-1}\]](/images/math/9/5/4/9545e792fdbd5ba5040c96ca7c289681.png)
![\[y=\ln\left(x+ \sqrt{x^{2}-1}\right)\]](/images/math/7/0/d/70df02ffaa30f6803bd61a55a9944595.png) A deriváltja
A deriváltja![\[\mbox{arcch}\,x=\ln\left(x+ \sqrt{x^{2}-1}\right)\]](/images/math/d/2/9/d29839c38c342f7cac32be4e509f8d95.png)
![\[\frac{d}{dx}\mbox{arcch}\,x=\frac{1}{\mbox{sh}(\mbox{arcsin}\,x)}=\frac{1}{\sqrt{x^{2}-1}}\,.\]](/images/math/b/a/c/bac64e65b1a10343c43876d7125b1d91.png)