Integrálás - Időfüggvények

Feladat

1. a) Az alábbi határozott integrál a változó felső $\setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0%$ határ miatt annak függvénye:

   $\[I(v)=\int_{0}^{v}\frac{1}{1-\alpha v'}dv'=t\]$

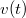   és egyenlő a $\setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0%$ időváltozóval. Határozzuk meg a $\setbox0\hbox{$v(t)$}% \message{//depth:\the\dp0//}% \box0%$ függvényt!

Megoldás

1. a)

   $\[t=\left[-\frac{1}{\alpha}\ln\left(1-\alpha v'\right)\right]^{v}_{0}\]$

   $\[-\alpha t=\ln(1-\alpha v)-\underbrace{\ln 1}_{0}\]$

   $\[e^{-\alpha t}=1-\alpha v\]$

   $\[v(t)=\frac{1}{\alpha}\left(1-e^{-\alpha t}\right)\]$