Kinematika - 1.3.1

Feladat

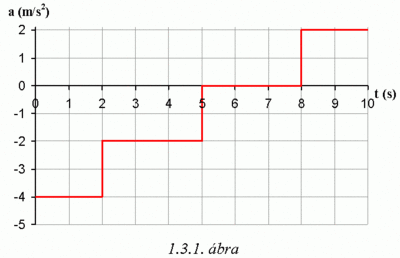
1. Az $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ tengelyen mozgó tömegpont gyorsulása az idő függvényében az 1.3.1. ábrán látható.
   

   a) Ábrázolja a tömegpont sebességét az idő függvényében, ha a kezdeti sebesség $\setbox0\hbox{$v_{0}=10 \,\mathrm{m/s}$}% \message{//depth:\the\dp0//}% \box0%$!

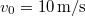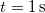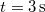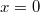   b) Határozza meg a tömegpont helyét a $\setbox0\hbox{$t=1 \,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$t=3 \,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ időpillanatokban, ha a tömegpont $\setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0%$-ban az $\setbox0\hbox{$x=0$}% \message{//depth:\the\dp0//}% \box0%$ pontban volt!

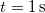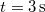   c) Mekkora a tömegpont átlagsebessége a $\setbox0\hbox{$t=1 \,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ és a $\setbox0\hbox{$t=3 \,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ közötti időintervallumban?

Megoldás

1. a) A feladatot az ábrán jelzett idő intervallumokon külön kell megoldani.
   
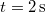   Itt az első két intervallumon történő számolást mutatjuk be. Az első intervallum $\setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0%$-tól $\setbox0\hbox{$t=2\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$-ig tart. Ezen a szakaszon 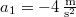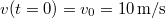$\setbox0\hbox{$a_{1}=-4\,\mathrm{\frac{m}{s^{2}}}$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$v(t=0)=v_{0}=10 \,\mathrm{m/s}$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$x(t=0)=0$}% \message{//depth:\the\dp0//}% \box0%$. 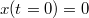A gyorsulás alapján a sebesség
   $\[v(0<t<2\,\mathrm{s})=v(0)+\int_{0}^{t}a(t')dt'=v_{0}+a_{1}t\]$
   szerint függ az időtől, melyet egy egyenes szakasszal ábrázolhatunk a sebesség-idő grafikonon. A hely idő függését az alábbiak szerint adhatjuk meg.
   $\[x(0<t<2\,\mathrm{s})=\underbrace{x(0)}_{0}+\int_{0}^{t}v(t')dt'=v_{0}t+\frac{a_{1}}{2}t^{2}\]$
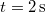   Ezek alapján az idő intervallum végén, vagyis a $\setbox0\hbox{$t=2\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ időpontban
   $\[v_{1}=v(t=2\,\mathrm{s})=2\,\mathrm{\frac{m}{s}}\qquad\qquad \mbox{és}\qquad\qquad x_{1}=x(t=2)=12\,\mathrm{m}\,.\]$
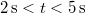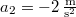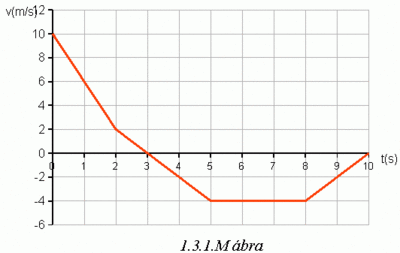
   Ezek az adatok jelentik a következő idő intervallum kezdeti feltételeit. A második intervallumon ($\setbox0\hbox{$2\,\mathrm{s}<t<5\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$) $\setbox0\hbox{$a_{2}=-2\,\mathrm{\frac{m}{s^{2}}}$}% \message{//depth:\the\dp0//}% \box0%$. Az első szakaszhoz hasonlóan
   $\[v(2\,\mathrm{s}<t<5\,\mathrm{s})=v(t=2\,\mathrm{s})+\int_{2\,\mathrm{s}}^{t}a(t')dt'=v_{1}+a_{2}(t-2\,\mathrm{s})\]$
   $\[x(2\,\mathrm{s}<t<5\,\mathrm{s})=x(t=2\,\mathrm{s})+\int_{2\,\mathrm{s}}^{t}v(t')dt'=x_{1}+v_{1}(t-2\,\mathrm{s})+\frac{a_{2}}{2}(t-2s)^{2}\,.\]$
   A többi idő intervallumon ugyanezeket a lépéseket kell megismételni. A kapott sebesség-idő grafikont az ÁBRÁn láthatjuk.

   b) Az a) rész eredményei alapján

   $\[x(t=1\,\mathrm{s})=6\,\mathrm{m}\qquad\mbox{és}\qquad x(t=3\,\mathrm{s})=4\,\mathrm{m}\,.\]$

   c) Az átlag sebesség a 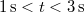$\setbox0\hbox{$1\,\mathrm{s}<t<3\,\mathrm{s}$}% \message{//depth:\the\dp0//}% \box0%$ intervallumon

   $\[v_{\mbox{átl}}=\frac{x(t=3\,\mathrm{s})-x(t=1\,\mathrm{s})}{3\,\mathrm{s}-1\,\mathrm{s}}=-1\,\mathrm{\frac{m}{s}}\,.\]$