Erőtan I. - 2.1.38
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. október 4., 14:38-kor történt szerkesztése után volt.
Feladat
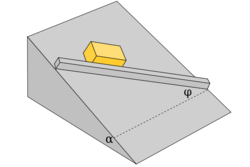
- (2.1.38) Az
 hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel
hajlásszögű lejtőre egy vékony lécet erősítünk úgy, hogy az a lejtőre illeszkedő vízszintes egyenessel  szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható
szöget zár be. A léc mellett csúszik egy tégla. Mekkora a gyorsulása, ha a csúszási súrlódási együttható 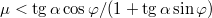 ?
?
Megoldás
- A testre ható gravitációs erőt először lejtőre merőleges (
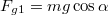 ) és azzal párhuzamos komponensre bontjuk fel (
) és azzal párhuzamos komponensre bontjuk fel (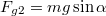 ). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő
). A lejtőre merőleges irányban nem történik mozgás ezért a lejtő 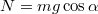 nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő
nyomóerővel nyomja a testet. A lejtővel párhuzamos síkban a gravitációs erő 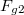 nagyságú komponensét felbontjuk egy a lécre merőleges (
nagyságú komponensét felbontjuk egy a lécre merőleges (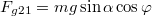 ) és a léccel párhuzamos irányú komponensre (
) és a léccel párhuzamos irányú komponensre (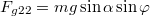 ). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet
). Ebben a síkban a lécre merőleges irányban sincs mozgás, ezért a léc a testet 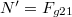 erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet amely meghatározza a test gyorsulását és ahol
erővel nyomja. A léccel párhuzamos irányba a mozgásegyenlet amely meghatározza a test gyorsulását és ahol![\[ma=F_{g22}-S-S'\,,\]](/images/math/6/7/c/67c3ab9275f54d04a98578dcb2827ce1.png)
 a lejtő által kifejtett súrlódási erő, míg
a lejtő által kifejtett súrlódási erő, míg 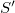 a léc által kifejtett súrlódási erő. A gyorsulás tehát
a léc által kifejtett súrlódási erő. A gyorsulás tehát![\[S=\mu N\qquad S'=\mu N' \qquad\qquad ma=mg\left[\sin\alpha\sin\varphi-\mu\left(\cos\alpha+\sin\alpha\cos\varphi\right)\right]\]](/images/math/1/b/e/1bee9499d34336f490ff9e9cfb799145.png)
![\[a=g\left[\sin\alpha\sin\varphi-\mu\left(\cos\alpha+\sin\alpha\cos\varphi\right)\right]\,.\]](/images/math/7/0/7/707e7922fdb2b659c31f114b54677e90.png)
- A testre ható gravitációs erőt először lejtőre merőleges (