Kinematika - 1.2.17

Feladat

1. (**1.2.17, csak csemegének) Egy 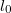$\setbox0\hbox{$l_{0}$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú, tökéletesen rugalmas és korlátlanul nyújtható fonál egyik végét falhoz rögzítjük. Erről a végpontról a fonálon mászva 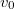$\setbox0\hbox{$v_{0}$}% \message{//depth:\the\dp0//}% \box0%$ sebességgel elindul egy hangya a másik vége felé. Ugyanabban a pillanatban azonban egy gonosz manó 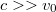$\setbox0\hbox{$c>>v_{0}$}% \message{//depth:\the\dp0//}% \box0%$ állandó sebességgel elkezdi húzni a fonál szabad végét. A hangyának a fonálhoz viszonyított sebessége az egész mozgás során állandó. Utolérheti-e a hangya a manót? (Mi történik, ha a hangya a manótól indul a fal felé?)

Megoldás

1. A fonál hosszúsága az idő függvényében
   $\[l(t)=l_{0}+ct\,,\]$
   mert a manó egyenletes sebességgel húzza.
   Ha a hangya faltól mért távolságát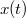 $\setbox0\hbox{$x(t)$}% \message{//depth:\the\dp0//}% \box0%$-vel jelöljük, akkor egy adott $\setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0%$ pillanatban a hangya lába alatt a fonál lokális sebessége
   $\[v_{fon}(t)=c\frac{x(t)}{l(t)}\,.\]$
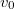   A hangya fonálhoz viszonyított sebessége mindig $\setbox0\hbox{$v_{0}$}% \message{//depth:\the\dp0//}% \box0%$, ezért a falhoz viszonyított sebesség
   $\[v(t)=v_{0}+v_{fon}(t)\]$
   $\[x'(t)=v_{0}+\frac{cx(t)}{l_{0}+ct}\,.\]$
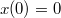   A kapott differenciálegyenletet az $\setbox0\hbox{$x(0)=0$}% \message{//depth:\the\dp0//}% \box0%$ kezdeti feltétellel kell megoldani. A megoldás
   $\[x(t)=\frac{v_{0}}{c}\left(l_{0}+ct\right)\mbox{ln}\left(\frac{l_{0}+ct}{l_{0}}\right)\]$
   alakban írható (érdemes az eredményt ellenőrizni a differenciálegyenletbe történő visszahelyettesítéssel).
   A feladatban az a kérdés, hogy a hangya és a manó közti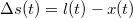 $\setbox0\hbox{$\Delta s(t)=l(t)-x(t)$}% \message{//depth:\the\dp0//}% \box0%$ távolság lecsökkenhet-e zérusra. Ha igen, akkor jelöljük $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$-vel azt az időpontot, amikor ez bekövetkezik.
   $\[\Delta s(T)=0\]$
   $\[T=\frac{l_{0}}{c}\left(e^{\frac{c}{v_{0}}}-1\right)\]$
   A hangya tehát minden esetben utoléri a manót.
   
   Ha a hangya a manótól indul, akkor a pillanatnyi sebessége
   $\[v(t)=-v_{0}+v_{fon}(t)\,.\]$
   $\[x'(t)=-v_{0}+\frac{cx(t)}{l_{0}+ct}\,,\]$
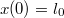   amelyet az $\setbox0\hbox{$x(0)=l_{0}$}% \message{//depth:\the\dp0//}% \box0%$ kezdeti feltétellel kell megoldani. A megoldás
   $\[x(t)=\frac{v_{0}}{c}(l_{0}+ct)\left[\frac{c}{v_{0}}+\mbox{ln}\left(\frac{l_{0}}{l_{0}+ct}\right)\right]\]$
   alapján meghatározhatjuk, hogy eléri-e a falat, vagyis létezik-e olyan $\setbox0\hbox{$T$}% \message{//depth:\the\dp0//}% \box0%$, melyre
   $\[x(T)=0\,.\]$
   $\[T=\frac{l_{0}}{c}\left(e^{\frac{c}{v_{0}}}-1\right)\]$
   A hangya tehát minden esetben eléri a falat.