Erőtan I. - 2.1.7

Feladat

1. Egy vasúti kocsi rakománya és a kocsi padlója közötti súrlódási együttható 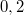$\setbox0\hbox{$0,2$}% \message{//depth:\the\dp0//}% \box0%$. A kocsi sebessége 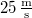$\setbox0\hbox{$25\,\mathrm{\frac{m}{s}}$}% \message{//depth:\the\dp0//}% \box0%$. Mekkora az a legrövidebb távolság, amelyen belül a kocsit a rakomány megcsúszásának veszélye nélkül állíthatjuk meg?

Megoldás

1. A fékezés során a rakományra ható erőket az ÁBRÁn ábrázoltuk.

ÁBRA

Függőleges irányban nem történik mozgás, ezért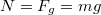 $\setbox0\hbox{$N=F_{g}=mg$}% \message{//depth:\the\dp0//}% \box0%$. Vízszintes irányban a tapadási erő hatására elkezd csökkenni a sebesség $\setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0%$ nagyságú gyorsulással. A tapadási erő a nyomóerővel van kapcsolatban.

$\[T\leq \mu N\]$

$\[a\leq \mu g\]$

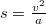A fékezés során $\setbox0\hbox{$s=\frac{v^{2}}{a}$}% \message{//depth:\the\dp0//}% \box0%$ utat tesz meg a test. Ezzel behelyettesítve

$\[s\geq \frac{v^{2}}{2\mu g}\,,\]$

vagyis megadtuk azt a feltételt, amely a ahhoz szükséges, hogy a rakomány ne csússzon meg a kocsin. A minimális út

$\[s_{min}=\frac{v^{2}}{2\mu g}=156,25\,\mathrm{m}\,.\]$