Erőtan I. - 2.1.9
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 12., 23:49-kor történt szerkesztése után volt.
Feladat
- Vízszintes deszkán fekszik egy nagy tömegű test. A deszka és a teher közötti súrlódási együttható
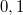 . Mekkora gyorsulást kell adnunk vízszintes irányban a deszkának, hogy a teher lemaradjon róla?
. Mekkora gyorsulást kell adnunk vízszintes irányban a deszkának, hogy a teher lemaradjon róla?
Megoldás
- A gyorsítás során a rakományra ható erőket az ÁBRÁn ábrázoltuk.
ÁBRA
Függőleges irányban nem történik mozgás, ezért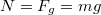 . Vízszintes irányban azt vizsgáljuk meg, hogy milyen gyorsulás lenne a legkisebb, amelyre még éppen nem csúszik meg a test. A tapadási erő a nyomóerővel van kapcsolatban.
. Vízszintes irányban azt vizsgáljuk meg, hogy milyen gyorsulás lenne a legkisebb, amelyre még éppen nem csúszik meg a test. A tapadási erő a nyomóerővel van kapcsolatban. ![\[T\leq \mu N\]](/images/math/7/7/5/7752e5d9457e3df8432246f73c90cb4a.png)
![\[a\leq \mu g\]](/images/math/4/0/e/40e8a98ae75821b3c361eca5e544d238.png)
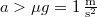 , akkor a test megcsúszik a deszkán.
, akkor a test megcsúszik a deszkán.