Erőtan I. - 2.1.16
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. április 22., 17:24-kor történt szerkesztése után volt.
Feladat
- Egy asztalon
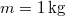 tömegű deszka, a deszkán
tömegű deszka, a deszkán 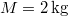 tömegű teher fekszik. Mekkora vízszintes irányú
tömegű teher fekszik. Mekkora vízszintes irányú  erővel kell hatni a deszkára, hogy az a teher alól kicsússzon? A teher és a deszka közötti tapadási-súrlódási együttható
erővel kell hatni a deszkára, hogy az a teher alól kicsússzon? A teher és a deszka közötti tapadási-súrlódási együttható 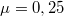 , a deszka és az asztal közötti tapadási-súrlódási együttható pedig
, a deszka és az asztal közötti tapadási-súrlódási együttható pedig 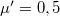 .
.
Megoldás
- Először vizsgáljuk meg, hogy mekkora az a maximális erő, melyre még éppen a deszka sem és a teher sem mozdulnak meg. A megoldás során a deszkára ható erők vessző nélküliek, míg a teherre ható erőket vesszővel jelöljük.
A teherre vonatkozó mozgásegyenletekA deszkára vonatkozó mozgásegyenletek![\[\mbox{függőleges}\qquad N'=F_{g}'=m'g\,.\]](/images/math/6/d/2/6d2c0aab52c799f45572394ce0475a84.png) Newton III. törvénye miatt
Newton III. törvénye miatt![\[\mbox{függőleges}\qquad N=F_{g}+G\qquad\qquad\mbox{vízszintes}\qquad F=T\,.\]](/images/math/9/c/c/9cc896e60f12dc5910cfe372e18c7444.png)
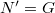 , így
, így 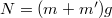 . A tapadási erő az alábbi összefüggésben van a nyomóerővel.
. A tapadási erő az alábbi összefüggésben van a nyomóerővel. ![\[\mu N\geq T\]](/images/math/8/a/2/8a25d1ed296e9f397028dee6a797e9dc.png) Tehát ha az erő kisebb, mint
Tehát ha az erő kisebb, mint![\[\mu(m+m')g\geq F\]](/images/math/c/1/9/c19892eabd34e544369a16d401c4f37a.png)
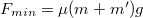 , akkor se a deszka, se a teher nem mozdulnak meg. Nagyobb erők esetén azonban már a deszka elkezd csúszni az asztalon.
, akkor se a deszka, se a teher nem mozdulnak meg. Nagyobb erők esetén azonban már a deszka elkezd csúszni az asztalon.
Tegyük fel egyelőre, hogy a teher még nem csúszik meg a deszkán, hanem együtt gyorsul azzal. A testekre vonatkozó függőleges irányú mozgásegyenletek megegyeznek a korábbiakkal, a vízszintes irányúak azonban![\[m'a=T'\]](/images/math/1/7/e/17ec273a8dba1f83dd339d39d31b5fff.png) szerint írhatóak fel, ahol
szerint írhatóak fel, ahol![\[ma=F-T'-S\]](/images/math/1/5/d/15d486e291131c9c93d50d71a3f9f535.png)
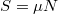 . A gyorsulás az elsőegyenlet alapján
. A gyorsulás az elsőegyenlet alapján 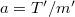 . Ezzel behelyettesítve a második egyenletbe a tapadási erő kifejezhető, amely a deszka és a teher közti nyomóerővel az alábbi kapcsolatban van.
. Ezzel behelyettesítve a második egyenletbe a tapadási erő kifejezhető, amely a deszka és a teher közti nyomóerővel az alábbi kapcsolatban van.![\[T'\frac{m}{m'}=F-T'-\mu(m+m')g\qquad\Rightarrow\qquad T'=\frac{Fm'}{m+m'}-\mu m'g\]](/images/math/2/0/d/20dc8b60f728b09e545707b52c8f2430.png)
![\[T'\leq\mu'N'\]](/images/math/2/b/4/2b4510947b3acd9580b7c260c0e684c2.png) Tehát ha a húzóerő kisebb, mint
Tehát ha a húzóerő kisebb, mint![\[F\leq(m+m')(\mu+\mu')g\]](/images/math/1/8/8/1887bf2f57ab92b8c1786a2829ae0c58.png)
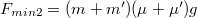 , akkor a teher nem csúszik meg a deszkán, hanem együtt gyorsul azzal. Az eddig meghatározott két erőre fennáll az
, akkor a teher nem csúszik meg a deszkán, hanem együtt gyorsul azzal. Az eddig meghatározott két erőre fennáll az 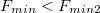 összefüggés, ezért ténylegesen lehetséges az imént bemutatott szituáció. Azonban ha a húzóerő nagyobb
összefüggés, ezért ténylegesen lehetséges az imént bemutatott szituáció. Azonban ha a húzóerő nagyobb 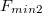 -nél, akkor a deszka kicsúszik a teher alól.
-nél, akkor a deszka kicsúszik a teher alól. ![\[F_{min2}=22,5\,\mathrm{N}\]](/images/math/f/9/8/f98f822c2d92d733c5e688dea45f5060.png)
- Először vizsgáljuk meg, hogy mekkora az a maximális erő, melyre még éppen a deszka sem és a teher sem mozdulnak meg. A megoldás során a deszkára ható erők vessző nélküliek, míg a teherre ható erőket vesszővel jelöljük.