Integrálás - Forgástest
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy parabola-antenna a nagy viharban leesett a háztetőről, és úgy ért a földre, hogy szimmetriatengelye éppen függőleges. A nagy esőben a tányér megtelt vízzel. Tudjuk, hogy a tányér mélysége középen
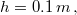 a tányér sugara pedig
a tányér sugara pedig 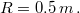
- a) Határozzuk meg, hogy mekkora térfogatú víz gyűlt össze a tányérban?
- b) Mekkora a tányér (belső) felülete?
Megoldás
- a) A parabola-tányér egy forgástest. Legyen a szimmetriatengely az
 tengely, a tányért úgy nyerjük, ha az
tengely, a tányért úgy nyerjük, ha az 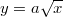 függvényt megforgatjuk az
függvényt megforgatjuk az  tengely körül. Az
tengely körül. Az  paramétert még meg kell határoznunk. Tudjuk, hogy az
paramétert még meg kell határoznunk. Tudjuk, hogy az 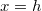 magasságnál a tányér sugara
magasságnál a tányér sugara  , azaz
, azaz
-
![\[a \sqrt{h} = R \quad \Rightarrow \quad a = \frac{R}{\sqrt{h}} \, .\]](/images/math/e/b/2/eb2aa7ca09e788a2d97c4b9a4e55fd3f.png)
- Tehát az
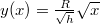 függvényt kell megforgatnunk. A tányér térfogata:
függvényt kell megforgatnunk. A tányér térfogata:
-
![\[ V = \int_{0}^{h} y(x)^2 \pi \,dx = \frac{R^2 \pi}{h} \int_0^h x \, dx = \frac{R^2 \pi}{h} \left[ \frac{x^2}{2} \right]_0^h = \frac{R^2 h \pi}{2} = 0.0393 m^3\]](/images/math/9/3/2/9327d7d554449cb2db6f2d7c6a2e88fd.png)
- b) A tányér felszínét az alábbi integrállal tudjuk meghatározni:
-
![\[ S = \int_0^h 2 \pi y(x) \sqrt{1 + y'(x)^2} \, dx = \frac{2 \pi R}{\sqrt{h}} \int_0^h \sqrt{x + \frac{R^2}{4 h}} \, dx = \]](/images/math/3/5/9/359b0b60871af78a067c9351a396ac6e.png)
-
![\[ = \frac{2 \pi R}{\sqrt{h}} \left[ \frac{2}{3} \left( x + \frac{R^2}{4 h} \right)^{3/2} \right]_0^h = \frac{4 \pi R}{3 \sqrt{h}} \left[ \left( h + \frac{R^2}{4 h} \right)^{3/2} - \left( \frac{R^2}{4 h} \right)^{3/2} \right] = 0.816 m^2 \]](/images/math/f/5/7/f576bdca19cbe3997cd0ca4b17276b20.png)
- a) A parabola-tányér egy forgástest. Legyen a szimmetriatengely az