„Integrálás - Területszámítás” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gyakor…”) |
|||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő:Gombkötő]] | [[Kategória:Szerkesztő:Gombkötő]] | ||
| + | [[Kategória:Mechanika]] | ||
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| 7. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># | + | </noinclude><wlatex># Határozzuk meg az $ f_1 (x) = cos x $ és az $ f_2 (x) = \sqrt{ 1 - x^2}$ függvéynek által közrefogott területet a [-1,1] intervallumon!</wlatex><includeonly><wlatex>{{Végeredmény|content=$T=2sin(1) - \frac{\pi}2$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>A keresett területet a $$T =\left| \int\limits _{-1} ^1 (f_1 (x) - f_2 (x) dx \right| $$ képlettel határozhatjuk meg. Mivel a függvények párosak, elegendő a [0,1] intervallumon vett területet nézni, illetve külön vizsgálhatjuk a két függvény alatti területeket, így $T=T_1-T_2$. Másrészt az $f_2$ görbe egy egység sugarú félkör, tehát $T_2=\pi/2$-t kell kapjunk. |
| + | |||
| + | Az 1. függvény primitívfüggvénye $F_1(x)=\sin x+c$, így $T_1=\sin(1)-\sin(-1)=2\sin(1)$. $F_2(x)$ meghatározásáhzo végezzük el az $x=\cos y$ helyettesítést: $$f_2 (y) = \sqrt{1- \cos^2 y} = |\sin y |,$$ de ha a párosság miatt csak a $0\le x \le 1$ intervallumon integrálunk, akkor $f_2 (y)=\sin y$, továbbá $$\frac {dx}{dy} = -\sin y,$$ $$dx= -\sin y dy ,$$ az új határok $x = 0$-nál $y =\frac { \pi}{2}$ és $x = 1 $-nél $y = 0$, ezzel $$\int\limits_ { x = 0} ^{ x = 1 } f_2 (x) dx = -\int\limits_ {y = \frac{ \pi}{2} } ^{ y = 0} \sin^2 y dy = \int\limits_ { \frac{ \pi}{2}} ^0 \left(\frac{\cos 2 y - 1}{2} \right) dy = \left[ \frac{\sin2y}{4} - \frac{y}{2} \right] _{ \frac{ \pi}{2}} ^0=0 + \frac { \ pi }{4},$$, ami a teljes intervallumon valóban $\pi/2$. Végül a keresett terület $$T=2sin(1)-\frac{\pi}{2}$$</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. május 31., 10:49-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozzuk meg az
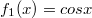 és az
és az 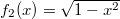 függvéynek által közrefogott területet a [-1,1] intervallumon!
függvéynek által közrefogott területet a [-1,1] intervallumon!
Megoldás
A keresett területet a![\[T =\left| \int\limits _{-1} ^1 (f_1 (x) - f_2 (x) dx \right| \]](/images/math/9/8/e/98ef683cb104be5255236e0b596edeca.png)
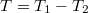 . Másrészt az
. Másrészt az 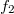 görbe egy egység sugarú félkör, tehát
görbe egy egység sugarú félkör, tehát 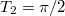 -t kell kapjunk.
Az 1. függvény primitívfüggvénye
-t kell kapjunk.
Az 1. függvény primitívfüggvénye 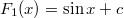 , így
, így 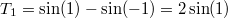 .
. 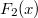 meghatározásáhzo végezzük el az
meghatározásáhzo végezzük el az 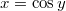 helyettesítést:
helyettesítést: ![\[f_2 (y) = \sqrt{1- \cos^2 y} = |\sin y |,\]](/images/math/5/e/6/5e6ddf870f71754aec4897a3a3493eb1.png)
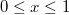 intervallumon integrálunk, akkor
intervallumon integrálunk, akkor 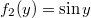 , továbbá
, továbbá ![\[\frac {dx}{dy} = -\sin y,\]](/images/math/4/d/3/4d39cd8cb014d7fd1cfdc44d4a2519cf.png)
![\[dx= -\sin y dy ,\]](/images/math/7/d/9/7d9bf718793591854798c78556e9857f.png)
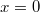 -nál
-nál 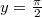 és
és 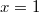 -nél
-nél 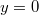 , ezzel
, ezzel ![\[\int\limits_ { x = 0} ^{ x = 1 } f_2 (x) dx = -\int\limits_ {y = \frac{ \pi}{2} } ^{ y = 0} \sin^2 y dy = \int\limits_ { \frac{ \pi}{2}} ^0 \left(\frac{\cos 2 y - 1}{2} \right) dy = \left[ \frac{\sin2y}{4} - \frac{y}{2} \right] _{ \frac{ \pi}{2}} ^0=0 + \frac { \ pi }{4},\]](/images/math/0/0/3/003bdebee7a335f30e80ee60a00f79d6.png)
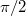 . Végül a keresett terület
. Végül a keresett terület ![\[T=2sin(1)-\frac{\pi}{2}\]](/images/math/4/8/c/48cf96de041ae005286cac93dbc7f5ca.png)