„Integrálás - Vegyes integrálok” változatai közötti eltérés
A Fizipedia wikiből
| 10. sor: | 10. sor: | ||
#: a) $$\int e^{x}\mbox{sh} x\,dx$$ | #: a) $$\int e^{x}\mbox{sh} x\,dx$$ | ||
#: b) $$\int\frac{1}{x^{2}+3}dx$$ | #: b) $$\int\frac{1}{x^{2}+3}dx$$ | ||
| − | #: c) $$\int_{0}^{\pi}\sin^{3}x\,dx$$</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $\frac{e^{2x}}{4}-\frac{x}{2}+C$ b) $\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C$ | + | #: c) $$\int_{0}^{\pi}\sin^{3}x\,dx$$</wlatex><includeonly><wlatex>{{Végeredmény|content=a) $\frac{e^{2x}}{4}-\frac{x}{2}+C$ b) $\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C$ c) $\frac43$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) $$\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C$$ | <wlatex>#: a) $$\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C$$ | ||
A lap 2013. március 28., 15:55-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Integrálás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozzuk meg az alábbi integrálokat lehetőség szerint többféle módszerrel!
- a)
![\[\int e^{x}\mbox{sh} x\,dx\]](/images/math/c/8/5/c85ec32a9805d564de6b373645ecf759.png)
- b)
![\[\int\frac{1}{x^{2}+3}dx\]](/images/math/1/6/2/1622a50694d6aad64f076ecc09655c73.png)
- c)
![\[\int_{0}^{\pi}\sin^{3}x\,dx\]](/images/math/c/d/b/cdb2462bda9b53c47163fb33bde41542.png)
- a)
Megoldás
- a)
![\[\int e^{x}\mbox{sh} x\,dx=\frac{e^{2x}}{4}-\frac{x}{2}+C\]](/images/math/c/d/c/cdc40363703b27cf9ac2fc8f728809e9.png)
- b) Mivel
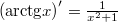, hasonló megoldást várunk. Az egyetlen eltérés ehhez képest a nevezőben a 3-as.Átalakítva az integrált bevezethetjük az![\[\frac{1}{3}\int\frac{1}{\frac{x^{2}}{3}+1}dx\]](/images/math/6/0/d/60d76fddfec4146e899adeb250bfd0bb.png)
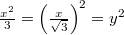azaz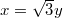 
helyettesítést. Ebből a transzformációs képletből: így az átírt integrál![\[\frac{dx}{dy}=\sqrt{3},\]](/images/math/4/6/2/4627bb36f49484989353b30c9296ed4d.png)
visszahelyettesítés után végül:![\[\frac{1}{3}\int\frac{1}{y^{2}+1}\sqrt{3}dx=\frac{1}{\sqrt{3}}\mbox{arctg}\,y+C\]](/images/math/f/7/9/f79464f3176e2849fc07dfbd72ce2a59.png)
![\[\frac{1}{\sqrt{3}}\mbox{arctg}\left(\frac{x}{\sqrt{3}}\right)+C\]](/images/math/1/7/a/17ae43437200f976baf5faea2bdad36f.png)
- c)
![\[\int_{0}^{\pi}\sin^{3}x\,dx=\int_{0}^{\pi}\sin^{2}x\sin x\,dx=\int_{0}^{\pi}\left(1-\cos^{2} x\right)\sin x\,dx=\int_{0}^{\pi}\sin x\,dx-\int_{0}^{\pi}\cos^{2}x\sin x\,dx=\]](/images/math/9/f/8/9f8202c00ad74720163447fda44cb38c.png)
- a)
![\[\left[-\cos x\right]^{\pi}_{0}+\left[\frac{\cos^{3} x}{3}\right]^{\pi}_{0}=\frac{4}{3}\]](/images/math/c/d/a/cdae33b69f3b5b4bc50e808f03f95857.png)
