Erőtan II. - Coriolis

Feladat

1. Egy $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ hosszúságú fonal végén $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű kicsiny test található. A fonal másik végét fogva, $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel forgatjuk a testet egy vízszintes, súrlódásmentes asztalon. Mekkora a kötélerő? Oldjuk meg a feladatot álló rendszerből nézve, ill az együttforgó rendszerből nézve is. Ezután oldjuk meg a feladatot valamely más 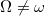$\setbox0\hbox{$\Omega \ne \omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel forgó rendszerből is! Milyen tehetetlenségi erők lépnek fel az egyes esetekben?

Megoldás

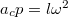1. Ha az álló rendszerből nézzük, úgy itt a test $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ körfrekvenciájú körmozgást végez. A centripetális gyorsulása $\setbox0\hbox{$a_cp = l \omega^2$}% \message{//depth:\the\dp0//}% \box0%$ a kör középpontja felé. A befelé ható kötélerő innen:

   $\[K = m l \omega^2 \; .\]$

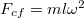   Ha beülünk az együttforgó koordinátarendszerbe, úgy azt látjuk, hogy a test áll, ezért rá az erőknek egyensúlyt kell tartani. Forgó koordinátarendszerben fellép a centrifugális erő, $\setbox0\hbox{$F_{cf} = m l \omega^2$}% \message{//depth:\the\dp0//}% \box0%$ kifelé. A test egyensúlya megköveteli, hogy befelé fellépjen egy

   $\[K = m l \omega^2\]$

   kötélerő.

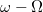   Ha egy $\setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel forgó koordinátarendszert veszünk, úgy a testet $\setbox0\hbox{$\omega - \Omega$}% \message{//depth:\the\dp0//}% \box0%$ szögsebességgel látjuk keringeni. Az egyszerűség kedvéért tegyük fel, hogy 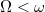$\setbox0\hbox{$\Omega < \omega$}% \message{//depth:\the\dp0//}% \box0%$, a másik eset teljesen hasonlóan tárgyalható. Ebben a rendszerben a test centripetális gyorsulása 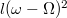$\setbox0\hbox{$l (\omega - \Omega)^2$}% \message{//depth:\the\dp0//}% \box0%$. A testre hat a centrifugális erő kifelé 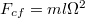$\setbox0\hbox{$F_{cf} = m l \Omega^2$}% \message{//depth:\the\dp0//}% \box0%$, ill. a Coriolis erő : 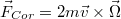$\setbox0\hbox{$\vec{F}_{Cor} = 2 m \vec{v} \times \vec{\Omega}$}% \message{//depth:\the\dp0//}% \box0%$, ami kiszámolva a keresztszorzatot 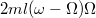$\setbox0\hbox{$2 m l (\omega - \Omega) \Omega$}% \message{//depth:\the\dp0//}% \box0%$ kifelé. Ebből

   $\[m a_{cp} = K - m l \Omega^2 - 2 m l (\omega - \Omega) \Omega \]$

   $\[ m l (\omega - \Omega)^2 = K - m l \Omega^2 - 2 m l (\omega - \Omega) \Omega \, ,\]$

   Átrendezve

   $\[K = m l \omega^2 \; .\]$

   Láthatjuk tehát, hogy a kötélerő nagysága nem függ a koordinátarendszer megválasztásától.