„Erőtan II. - 4.37” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
(→Megoldás) |
||
| 12. sor: | 12. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: A $v$ sebességű részecskéknek $\Delta t=\frac{R-r}{v}$ időre van szükségük. Ezalatt a rendszer $$\varphi=\omega\Delta t$$ szöget fordul el. Így az állóhelyzethez képest a becsapódás helyét meghatározó ívhossz $$i=R\varphi=R\omega\frac{R-r}{v}\,.$$ | + | <wlatex>#: A $v$ sebességű részecskéknek $\Delta t=\frac{R-r}{v}$ időre van szükségük. Ezalatt a rendszer $$\varphi=\omega\Delta t$$ szöget fordul el. Így az állóhelyzethez képest a becsapódás helyét meghatározó ívhossz $$i=R\varphi=R\omega\frac{R-r}{v}\,.$$[[Kép:Kfgy1_05_4_37m.svg|none|250px]] |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2013. június 20., 10:59-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
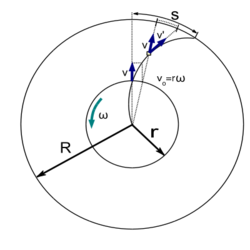
- Egy gázban a molekulák sebességeloszlásának meghatározására a következő mérést végezhetjük (Stern kísérlet). Egy izzítható fémszálat körülveszünk két koaxiális hengerrel, amelyek sugarai
és 
. A belsőn az egyik alkotóján egy keskeny rést hozunk létre. Ha az egész rendszer nyugalomban van, az elpárolgó fém molekulái a réssel szemben a külső henger falán egy egyenes vonal mentén csapódnak le. Ha az egész rendszert 
szögsebességgel forgatjuk, a becsapódó molekulák sebességüktől függő mértékben jobban vagy kevésbé eltérnek ettől a vonaltól. Számítsuk ki az eltérés ívhosszát a részecskék sebességének függvényében!
Megoldás
- A
sebességű részecskéknek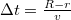 
időre van szükségük. Ezalatt a rendszer szöget fordul el. Így az állóhelyzethez képest a becsapódás helyét meghatározó ívhossz![\[\varphi=\omega\Delta t\]](/images/math/0/4/d/04d5d4154070f9efb50f71c64e221806.png)
![\[i=R\varphi=R\omega\frac{R-r}{v}\,.\]](/images/math/0/8/8/088015d84b0c7f3a94f7f70e4ce0b0a2.png)
- A
