„Erőtan II. - 4.8” változatai közötti eltérés
A Fizipedia wikiből
| (3 szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
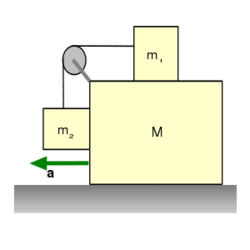
| − | </noinclude><wlatex># | + | </noinclude><wlatex># (4.8) Mekkora gyorsulással kell az $M$ tömeget mozgatni, hogy hozzá képest az $m_{1}$ és $m_{2}$ tömegű testek nyugalomban legyenek? A kötél nyújthatatlan és elhanyagolható tömegű, súrlódás sehol nincs. (4.8. ábra) [[Kép:Kfgy1_05_4_8.svg|none|250px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a testekre ható erőket!}}{{Végeredmény|content=$$a=\frac{m_{2}}{m_{1}}g$$}}</wlatex></includeonly><noinclude> |
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a testekre ható erőket!}}{{Végeredmény|content=$$a=\frac{m_{2}}{m_{1}}g$$}}</wlatex></includeonly><noinclude> | + | |
== Megoldás == | == Megoldás == | ||
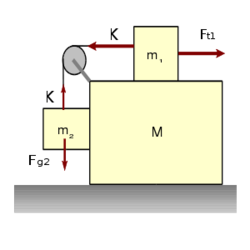
<wlatex>#: Az $m_{1}$ és $m_{2}$ tömegű testekre ható erőket az ábrán ábrázoltuk. (Nem az összes fellépő erőt jelöltük be, csak amelyek a megoldásban szerepet játszanak.) | <wlatex>#: Az $m_{1}$ és $m_{2}$ tömegű testekre ható erőket az ábrán ábrázoltuk. (Nem az összes fellépő erőt jelöltük be, csak amelyek a megoldásban szerepet játszanak.) | ||
| − | + | [[Kép:4.8M.svg|none|250px]] | |
Egyensúlyi esetben $$F_{g2}=K=F_{t1}$$ $$m_{2}g=m_{1}a\qquad\Rightarrow\qquad a=\frac{m_{2}}{m_{1}}g\,.$$ | Egyensúlyi esetben $$F_{g2}=K=F_{t1}$$ $$m_{2}g=m_{1}a\qquad\Rightarrow\qquad a=\frac{m_{2}}{m_{1}}g\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 27., 21:26-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (4.8) Mekkora gyorsulással kell az
tömeget mozgatni, hogy hozzá képest az 
és 
tömegű testek nyugalomban legyenek? A kötél nyújthatatlan és elhanyagolható tömegű, súrlódás sehol nincs. (4.8. ábra) 
Megoldás
- Az és tömegű testekre ható erőket az ábrán ábrázoltuk. (Nem az összes fellépő erőt jelöltük be, csak amelyek a megoldásban szerepet játszanak.)
- Az
![\[F_{g2}=K=F_{t1}\]](/images/math/0/4/9/049ec49dc8a3b3a2e3bc37c00f31a23d.png)
![\[m_{2}g=m_{1}a\qquad\Rightarrow\qquad a=\frac{m_{2}}{m_{1}}g\,.\]](/images/math/8/a/a/8aa718c9edac46f815026f4388738fbf.png)
