„Mechanika - Áramlás csőben” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
(→Megoldás) |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (5.10.) Egy vékony cső keresztmetszete adott $f(x)$ függvény szerint változik ($x$ a cső tengelye mentén mért távolság). Hogyan változik a cső mentén az áramló folyadék nyomása és sebessége?</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk Bernoulli-törvényét ideális folyadéra!}}{{Végeredmény|content=$$v(x)=\frac{f(0)v(0)}{f(x)}$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># (5.10.) Egy vékony cső keresztmetszete adott $f(x)$ függvény szerint változik ($x$ a cső tengelye mentén mért távolság). Hogyan változik a cső mentén az áramló folyadék nyomása és sebessége?</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk Bernoulli-törvényét ideális folyadéra!}}{{Végeredmény|content=$$v(x)=\frac{f(0)v(0)}{f(x)}$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>Bernoulli-törvényét alkalmazzuk feltéve, hogy a cső vízszintes, tehát nincs magasságfüggő tagja a hidrosztatikai nyomásnak: $$\frac{\rho v^2(0)}2+p(0)=\frac{\rho v^2(x)}2+p(x)$$ Összenyomhatatlan folyadékra nem csak a tömegáram, hanem a térfogatáram is állandó minden kereszmetszetben, azaz $f(x)v(x)=\text{áll.}$. Ebből $$v(x)=\frac{f(0)v(0)}{f(x)}$$ Ezt négyzetre emelve helyettesíthetünk be a Bernoulli-törvénybe, melyből $p(x) | + | <wlatex>Bernoulli-törvényét alkalmazzuk feltéve, hogy a cső vízszintes, tehát nincs magasságfüggő tagja a hidrosztatikai nyomásnak: $$\frac{\rho v^2(0)}2+p(0)=\frac{\rho v^2(x)}2+p(x)$$ Összenyomhatatlan folyadékra nem csak a tömegáram, hanem a térfogatáram is állandó minden kereszmetszetben, azaz $f(x)v(x)=\text{áll.}$. Ebből $$v(x)=\frac{f(0)v(0)}{f(x)}$$ Ezt négyzetre emelve helyettesíthetünk be a Bernoulli-törvénybe, melyből $$p(x)=\frac{\rho v^2(0)}2+p(0)-\frac{\rho v^2(0)f^2(0)}{2f^2(x)}.$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. november 18., 23:30-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.10.) Egy vékony cső keresztmetszete adott
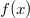függvény szerint változik (
a cső tengelye mentén mért távolság). Hogyan változik a cső mentén az áramló folyadék nyomása és sebessége?
Megoldás
Bernoulli-törvényét alkalmazzuk feltéve, hogy a cső vízszintes, tehát nincs magasságfüggő tagja a hidrosztatikai nyomásnak:![\[\frac{\rho v^2(0)}2+p(0)=\frac{\rho v^2(x)}2+p(x)\]](/images/math/d/7/8/d78657d4d305938636f351bca9bfc2d3.png)
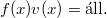. Ebből ![\[v(x)=\frac{f(0)v(0)}{f(x)}\]](/images/math/d/1/d/d1d92d23fd1c053500f11898222153ae.png)
![\[p(x)=\frac{\rho v^2(0)}2+p(0)-\frac{\rho v^2(0)f^2(0)}{2f^2(x)}.\]](/images/math/4/a/b/4ab9d4455a811b4bf32e6cb80e084085.png)
