„Erőtan II. - 4.4” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Erőtan II. {{Kísérleti fizika gyakorlat …”) |
(→Feladat) |
||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy $l$ hosszúságú, $m$ tömegű matematikai ingát mérlegre állítunk. Ha az inga legnagyobb kitérésekor a függőlegessel bezárt szöge $\varphi_{0}$, számítsuk ki, mekkora az inga súlya abban a pillanatban, amikor a függőlegessel bezárt szöge $\varphi$. | + | </noinclude><wlatex># (*4.4) Egy $l$ hosszúságú, $m$ tömegű matematikai ingát mérlegre állítunk. Ha az inga legnagyobb kitérésekor a függőlegessel bezárt szöge $\varphi_{0}$, számítsuk ki, mekkora az inga súlya abban a pillanatban, amikor a függőlegessel bezárt szöge $\varphi$. |
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$G=mg\cos\varphi\big(3\cos\varphi-2\cos\varphi_{0}\big)$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$G=mg\cos\varphi\big(3\cos\varphi-2\cos\varphi_{0}\big)$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: Az test sebessége egy adott $\varphi$ kitérés esetén energetikai megfontolásokkal adható meg. $$mgl(1-\cos\varphi_{0})=mgl(1-\cos\varphi)+\frac{1}{2}mv(\varphi)^{2}$$ Egy adott $\varphi$ szögnél a testre kötél irányban ható erők a kötélerő és a gravitációs erő kötéllel párhuzamos komponense, melynek nagysága $F_{g}\cos\varphi$. A két erő eredőjének kell a centripetális erő szerepét játszania, vagyis | + | <wlatex>#: Az test sebessége egy adott $\varphi$ kitérés esetén energetikai megfontolásokkal adható meg. $$mgl(1-\cos\varphi_{0})=mgl(1-\cos\varphi)+\frac{1}{2}mv(\varphi)^{2}$$ Egy adott $\varphi$ szögnél a testre kötél irányban ható erők a kötélerő és a gravitációs erő kötéllel párhuzamos komponense, melynek nagysága $F_{g}\cos\varphi$. A két erő eredőjének kell a centripetális erő szerepét játszania, vagyis $$m\frac{v(\varphi)^{2}}{l}=K-mg\cos\varphi$$ Behelyettesítve a sebesség korábban kapott formulájával $$K=mg\big(3\cos\varphi-2\cos\varphi_{0}\big)\,.$$ Az ingát tartó szerkezetre a kötélerő ellenereje hat, illetve a mérleg tartja. A $K$ kötélerő vízszintes komponensét a mérleg és a tartó szerkezet közti tapadási erő egyenlíti ki, míg a függőleges komponensét a nyomóerő, mely megegyezik a mérlegre ható súlyerővel. $$G=N=K\cos\varphi=mg\cos\varphi\big(3\cos\varphi-2\cos\varphi_{0}\big)$$ |
| − | $$m\frac{v(\varphi)^{2}}{l}=K-mg\cos\varphi$$ Behelyettesítve a sebesség korábban kapott formulájával $$K=mg\big(3\cos\varphi-2\cos\varphi_{0}\big)\,.$$ Az ingát tartó szerkezetre a kötélerő ellenereje hat, illetve a mérleg tartja | + | |
| − | + | ||
| − | A $K$ | + | |
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 9., 15:31-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*4.4) Egy
hosszúságú, 
tömegű matematikai ingát mérlegre állítunk. Ha az inga legnagyobb kitérésekor a függőlegessel bezárt szöge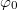 
, számítsuk ki, mekkora az inga súlya abban a pillanatban, amikor a függőlegessel bezárt szöge 
.
Megoldás
- Az test sebessége egy adott kitérés esetén energetikai megfontolásokkal adható meg. Egy adott
![\[mgl(1-\cos\varphi_{0})=mgl(1-\cos\varphi)+\frac{1}{2}mv(\varphi)^{2}\]](/images/math/a/3/b/a3b4abe613d9a4987b1c7898dbb0eb02.png)
szögnél a testre kötél irányban ható erők a kötélerő és a gravitációs erő kötéllel párhuzamos komponense, melynek nagysága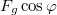 
. A két erő eredőjének kell a centripetális erő szerepét játszania, vagyis Behelyettesítve a sebesség korábban kapott formulájával![\[m\frac{v(\varphi)^{2}}{l}=K-mg\cos\varphi\]](/images/math/9/a/8/9a84b457e2189dbe5ea711456024fd9a.png)
Az ingát tartó szerkezetre a kötélerő ellenereje hat, illetve a mérleg tartja. A![\[K=mg\big(3\cos\varphi-2\cos\varphi_{0}\big)\,.\]](/images/math/2/5/c/25cf0a49e2eac20fa9b744cb227da629.png)
kötélerő vízszintes komponensét a mérleg és a tartó szerkezet közti tapadási erő egyenlíti ki, míg a függőleges komponensét a nyomóerő, mely megegyezik a mérlegre ható súlyerővel. ![\[G=N=K\cos\varphi=mg\cos\varphi\big(3\cos\varphi-2\cos\varphi_{0}\big)\]](/images/math/b/0/2/b029a6689bdeaf148b408697aab3cbb4.png)
- Az test sebessége egy adott
