„Deriválás - Inverz függvény deriváltja” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># * Tegyük fel, hogy ismerjük egy $f(x)$ függvény deriváltját. Ekkor az $f(x)$ függvény $\phi(x)$ inverzének deriváltja $$\frac{d\phi}{dx}=\frac{1}{f'(\phi(x))}\,.$$ Ennek segítségével számítsuk ki az alábbi függvények deriváltját. | </noinclude><wlatex># * Tegyük fel, hogy ismerjük egy $f(x)$ függvény deriváltját. Ekkor az $f(x)$ függvény $\phi(x)$ inverzének deriváltja $$\frac{d\phi}{dx}=\frac{1}{f'(\phi(x))}\,.$$ Ennek segítségével számítsuk ki az alábbi függvények deriváltját. | ||
| − | #: a) $\mbox{ | + | #: a) $\mbox{ln}\,x$ |
| − | #: b) $\mbox{ | + | #: b) $\mbox{arcsin}\,x$ |
| − | #: c) $\mbox{ | + | #: c) $\mbox{arccos}\,x$ |
| − | #: d) $\mbox{ | + | #: d) $\mbox{arctg}\,x$ |
| − | #: e) $\mbox{arcsin}\left(e^{x}+x^{2}\sin x\right)$ | + | #: e) $\mbox{arcctg}\,x$ |
| − | #: | + | #: f) $\mbox{arcsin}\left(e^{x}+x^{2}\sin x\right)$ |
| + | #: g) $\mbox{arctg}\,\left[2\ln x+\sin(\cos x)\right]$</wlatex><includeonly></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) $$\frac{d}{dx}\mbox{arcsin}\,x=\frac{1}{\cos(\mbox{arcsin}\,x)}=\frac{1}{\sqrt{1-x^{2}}}$$ | <wlatex>#: a) $$\frac{d}{dx}\mbox{arcsin}\,x=\frac{1}{\cos(\mbox{arcsin}\,x)}=\frac{1}{\sqrt{1-x^{2}}}$$ | ||
A lap 2014. szeptember 8., 16:18-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Deriválás |
Feladatok listája:
|
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- * Tegyük fel, hogy ismerjük egy
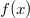függvény deriváltját. Ekkor az 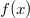függvény 
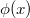inverzének deriváltja Ennek segítségével számítsuk ki az alábbi függvények deriváltját.![\[\frac{d\phi}{dx}=\frac{1}{f'(\phi(x))}\,.\]](/images/math/a/9/6/a96c3eb71530a906e1ec6e66c86c4547.png)
- a)
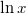
- b)
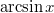
- c)
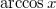
- d)
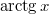
- e)
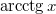
- f)
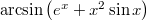
- g)
![\setbox0\hbox{$\mbox{arctg}\,\left[2\ln x+\sin(\cos x)\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/1/4/c/14cd40276978bdfe1d816408051167c7.png)
- a)
Megoldás
- a)
![\[\frac{d}{dx}\mbox{arcsin}\,x=\frac{1}{\cos(\mbox{arcsin}\,x)}=\frac{1}{\sqrt{1-x^{2}}}\]](/images/math/e/5/b/e5b45290611592b2b858754045af2e66.png)
- b)
![\[\frac{d}{dx}\mbox{arccos}\,x=-\frac{1}{\sqrt{1-x^{2}}}\]](/images/math/f/4/3/f4369bf956e7c16ede2101fd5aee7a1b.png)
- c)
![\[\frac{d}{dx}\mbox{arctg}\,x=\cos^{2}(\mbox{arctg}\,x)=\frac{1}{1+x^{2}}\]](/images/math/2/4/c/24c9a54d689a7ec9919dbacf08ccc8d8.png)
- d)
![\[\frac{d}{dx}\mbox{arcctg}\,x=-\frac{1}{1+x^{2}}\]](/images/math/4/9/b/49b62b8a39b8b37bce9535f94cb60d29.png)
- e)
![\[\frac{d}{dx}\mbox{arcsin}\left(e^{x}+x^{2}\sin x\right)=\frac{e^{x}+2x\sin x+x^{2}\cos x}{\sqrt{1-\left(e^{x}+x^{2}\sin x\right)^{2}}}\]](/images/math/d/1/9/d193b4bcfec2b10d8b64b3dc99c3b9fd.png)
- f)
![\[\frac{d}{dx}\mbox{arctg}\,\left[2\ln x+\sin(\cos x)\right]=\frac{\frac{2}{x}-\sin x\cos(\cos x)}{1+\left[2\ln x+\sin(\cos x)\right]^{2}}\]](/images/math/0/0/0/000f53b36afc8d49a7feef2336df01c7.png)
- a)
