„Erőtan I. - Futószalag” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő 3 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
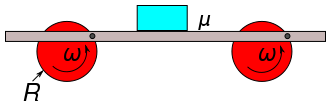
| − | </noinclude><wlatex># Egy gyárban egy érdekes futószalagot látunk. A futószalag egy vízszintes lap, amit $R$ sugarú kerekek együttes forgatása mozgat. A lap mindig vízszintes. Rajta nyugszik egy kicsiny test, a lap és a test között a súrlódási együttható $\mu$. | + | </noinclude><wlatex># Egy gyárban egy érdekes futószalagot látunk. A futószalag egy vízszintes lap, amit $R$ sugarú kerekek együttes forgatása mozgat. A lap mindig vízszintes. Rajta nyugszik egy kicsiny test, a lap és a test között a súrlódási együttható $\mu$. |
| − | #: a.) | + | #: a.) Legfeljebb mekkora legyen a szögsebesség, ha nem szeretnénk, hogy a test elváljon a laptól? |
| − | #: b.) | + | #: b.) Legalább mekkora legyen a kerekek szögsebessége, ha szeretnénk, hogy a test megcsússzon a lapon? |
| − | #: c.) Kvalitative milyen mozgást végez a test? | + | #: c.) Kvalitative milyen mozgást végez a test? |
[[Fájl:futoszalag.svg]] | [[Fájl:futoszalag.svg]] | ||
</wlatex><includeonly><wlatex>{{Végeredmény|content= Majd lesz}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content= Majd lesz}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | + | <wlatex>#: a.) Ha a test nem válik el a laptól, akkor a függőleges koordinátájának időfüggése: $$y(t) = R \sin (\omega t + \varphi) \, ,$$ ahol $\varphi$ valamilyen (számunkra most lényegtelen) kezdőfázis. Deriváljuk ezt kétszer idő szerint! $$a_y(t) = - R \omega^2 \sin(\omega t + \varphi) \, . $$ Akkor nem válik el a laptól, ha a függőleges gyorsulás maximuma kisebb mint $g$, ebből $R \omega^2 < g$, vagyis $$\omega < \sqrt{\frac{g}{R}} \; .$$ | |
| − | <wlatex>#: A | + | #: b.) A feladat megválaszolásához először tegyük fel, hogy a test nem csúszik meg. Ekkor a koordinátáinak időfüggése ($\varphi = 0$ az egyszerűség kedvéért.): $$y(t) = R \sin (\omega t) \, ,$$ $$x(t) = R \cos(\omega t) \, .$$ A gyorsulás függőleges komponense: $$a_y(t) = - R \omega^2 \sin(\omega t) \, , $$ ebből a nyomóerő időfüggése $$N = m a_y + m g = - m R \omega^2 \sin(\omega t) + m g \, .$$ Feltéve, hogy az a.) feladatban kapottnál kisebb az $omega$, ez biztosan pozitív. |
| + | #: A gyorsulás vízszintes komponense $$a_x(t) = - R \omega^2 \cos(\omega t) \, .$$ Ezt a tapadási súrlódási erő hozza létre, azaz $$ T = - m R \omega^2 \cos(\omega t)$$. A test akkor csúszik meg, ha ez nagyobb, mint $\mu N$, azaz $$ |T| > \mu N$$ $$ m R \omega^2 |\cos(\omega t)| > \mu m g - \mu m R \omega^2 \sin(\omega t) \, .$$ Arról hamar meggyőződhetünk, hogy megcsúszástól akkor kell | ||
| + | tartanunk először, amikor a test épp... | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. november 10., 19:01-kori változata
Feladat
- Egy gyárban egy érdekes futószalagot látunk. A futószalag egy vízszintes lap, amit
sugarú kerekek együttes forgatása mozgat. A lap mindig vízszintes. Rajta nyugszik egy kicsiny test, a lap és a test között a súrlódási együttható 
.
- a.) Legfeljebb mekkora legyen a szögsebesség, ha nem szeretnénk, hogy a test elváljon a laptól?
- b.) Legalább mekkora legyen a kerekek szögsebessége, ha szeretnénk, hogy a test megcsússzon a lapon?
- c.) Kvalitative milyen mozgást végez a test?
Megoldás
- a.) Ha a test nem válik el a laptól, akkor a függőleges koordinátájának időfüggése: ahol
![\[y(t) = R \sin (\omega t + \varphi) \, ,\]](/images/math/6/5/1/651d4d34e2b644f0432dbbbc5a6aae92.png)
valamilyen (számunkra most lényegtelen) kezdőfázis. Deriváljuk ezt kétszer idő szerint! Akkor nem válik el a laptól, ha a függőleges gyorsulás maximuma kisebb mint![\[a_y(t) = - R \omega^2 \sin(\omega t + \varphi) \, . \]](/images/math/6/9/6/696b5b9f2b833f791ebd5547f988d3fe.png)
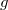, ebből 
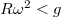, vagyis ![\[\omega < \sqrt{\frac{g}{R}} \; .\]](/images/math/3/7/0/3708dc8863a484627e830c4d7a117059.png)
- b.) A feladat megválaszolásához először tegyük fel, hogy a test nem csúszik meg. Ekkor a koordinátáinak időfüggése (
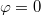az egyszerűség kedvéért.): ![\[y(t) = R \sin (\omega t) \, ,\]](/images/math/c/b/7/cb77fa78ca4676862661a9dcbdbddf3e.png)
A gyorsulás függőleges komponense:![\[x(t) = R \cos(\omega t) \, .\]](/images/math/1/2/2/122ab0d12812cb62f655196217ee1c55.png)
ebből a nyomóerő időfüggése![\[a_y(t) = - R \omega^2 \sin(\omega t) \, , \]](/images/math/9/c/5/9c5a9aca7c1de1891957a05daf0b6247.png)
Feltéve, hogy az a.) feladatban kapottnál kisebb az![\[N = m a_y + m g = - m R \omega^2 \sin(\omega t) + m g \, .\]](/images/math/6/f/b/6fbea94bdbb5c9d15796b0d0ac7cacfc.png)
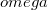, ez biztosan pozitív.
- A gyorsulás vízszintes komponense Ezt a tapadási súrlódási erő hozza létre, azaz
![\[a_x(t) = - R \omega^2 \cos(\omega t) \, .\]](/images/math/5/f/4/5f42b24e026b72313d5039a2a9333092.png)
. A test akkor csúszik meg, ha ez nagyobb, mint![\[ T = - m R \omega^2 \cos(\omega t)\]](/images/math/2/b/f/2bfdda83c31d65f2242e8bae96daba63.png)
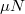, azaz ![\[ |T| > \mu N\]](/images/math/6/a/f/6af818850d8efa75f17d134219cd3c63.png)
Arról hamar meggyőződhetünk, hogy megcsúszástól akkor kell![\[ m R \omega^2 |\cos(\omega t)| > \mu m g - \mu m R \omega^2 \sin(\omega t) \, .\]](/images/math/a/2/1/a219bbe2dbed7aba8f111a346a0180ea.png)
- a.) Ha a test nem válik el a laptól, akkor a függőleges koordinátájának időfüggése:
tartanunk először, amikor a test épp...
