„Mechanika - Folyadékóra” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
a |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (5.11.) A homokóra mintájára "folyadékórát" készítünk. A folyadékóra tartályának alján kicsi, $A$ keresztmetszetű lyukon folyik ki a folyadék. Milyen alakú forgástestté kell kiképezni az edényt, ha azt akarjuk, hogy a folyadék felszíne állandó $v_0$ sebességgel süllyedjen?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$h(r)=\frac{v_0^2}{2g}\left(\frac{\pi^2r^4}{A^2}-1\right)$$}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># (5.11.) A homokóra mintájára "folyadékórát" készítünk. A folyadékóra tartályának alján kicsi, $A$ keresztmetszetű lyukon folyik ki a folyadék. Milyen alakú forgástestté kell kiképezni az edényt, ha azt akarjuk, hogy a folyadék felszíne állandó $v_0$ sebességgel süllyedjen?</wlatex><includeonly><wlatex>{{Végeredmény|content=$$h(r)=\frac{v_0^2}{2g}\left(\frac{\pi^2r^4}{A^2}-1\right)$$}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A tartály alakját leíró $h(r)$ függvényt, vagy annak inverzét keressük, ahol $r$ az erény sugara a kifolyó nyílás felett $h$ magasságban. A térfogatáram állandósága $$Av= | + | <wlatex>A tartály alakját leíró $h(r)$ függvényt, vagy annak inverzét keressük, ahol $r$ az erény sugara a kifolyó nyílás felett $h$ magasságban. A térfogatáram állandósága $$Av=r^2\pi v_0,$$ továbbá a Bernoulli-egyenlet $$\frac12\rho v^2=\frac12\rho v_0^2+\rho gh$$ egymásba helyettesítve $v$ kiejtésével teremt kapcsolatot a két mennyiség között. Ezekből $$h(r)=\frac{v_0^2}{2g}\left(\frac{\pi^2r^4}{A^2}-1\right)$$ egy invertálható függvény.</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2015. november 11., 13:50-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.11.) A homokóra mintájára "folyadékórát" készítünk. A folyadékóra tartályának alján kicsi,
keresztmetszetű lyukon folyik ki a folyadék. Milyen alakú forgástestté kell kiképezni az edényt, ha azt akarjuk, hogy a folyadék felszíne állandó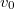 
sebességgel süllyedjen?
Megoldás
A tartály alakját leíró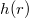
függvényt, vagy annak inverzét keressük, ahol 
az erény sugara a kifolyó nyílás felett 
magasságban. A térfogatáram állandósága ![\[Av=r^2\pi v_0,\]](/images/math/f/0/7/f070abdceed2fe16f859409fe2e29500.png)
![\[\frac12\rho v^2=\frac12\rho v_0^2+\rho gh\]](/images/math/3/a/b/3ab79ec5aa3fb1e5c0d0ddba1c3b2985.png)
kiejtésével teremt kapcsolatot a két mennyiség között. Ezekből ![\[h(r)=\frac{v_0^2}{2g}\left(\frac{\pi^2r^4}{A^2}-1\right)\]](/images/math/4/f/f/4ff9fbce26228db79c8e2adcfe104bbe.png)
