„Erőtan II. - 4.24” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (4.24) Az Egyenlítőn fekvő repülőtéren három teljesen egyforma ingaóra van. Az $A$ ingaóra a repülőtéren marad, a $K$ ingaórát egy kelet, a $NY$-t egy nyugat felé induló repülőgépre helyezik. Pontosan délben - amikor mindhárom óra ugyanazt az időt mutatja - a repülőgépek elindulnak és egyenletes sebességgel körberepülik a Földet, úgy, hogy egyszerre érjenek vissza a kiindulási repülőtérre. Visszaérkezésükkor az $A$ óra éppen következő nap déli 12 óra 0 perc 0 másodpercet mutat. | + | </noinclude><wlatex># (*4.24) Az Egyenlítőn fekvő repülőtéren három teljesen egyforma ingaóra van. Az $A$ ingaóra a repülőtéren marad, a $K$ ingaórát egy kelet, a $NY$-t egy nyugat felé induló repülőgépre helyezik. Pontosan délben - amikor mindhárom óra ugyanazt az időt mutatja - a repülőgépek elindulnak és egyenletes sebességgel körberepülik a Földet, úgy, hogy egyszerre érjenek vissza a kiindulási repülőtérre. Visszaérkezésükkor az $A$ óra éppen következő nap déli 12 óra 0 perc 0 másodpercet mutat. |
#: a) Mindhárom óra ugyanezt az időt mutatja-e? Ha nem, soroljunk fel különböző okokat, melyek az időkülönbséget előidézhetik! | #: a) Mindhárom óra ugyanezt az időt mutatja-e? Ha nem, soroljunk fel különböző okokat, melyek az időkülönbséget előidézhetik! | ||
#: b) A legjelentősebb hatás figyelembevételével adjuk meg, hogy mennyivel fog többet, illetve kevesebbet mutatni a $K$, illetve az $NY$ óra a 24 órás repülés után! | #: b) A legjelentősebb hatás figyelembevételével adjuk meg, hogy mennyivel fog többet, illetve kevesebbet mutatni a $K$, illetve az $NY$ óra a 24 órás repülés után! | ||
</wlatex><includeonly><wlatex>{{Végeredmény|content=$$t_{K}=1 \,\mathrm{nap} - 7,33 \,\mathrm{perc}\qquad\qquad t_{NY}=1 \,\mathrm{nap} + 4,87 \,\mathrm{perc}$$}}</wlatex></includeonly><noinclude> | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$t_{K}=1 \,\mathrm{nap} - 7,33 \,\mathrm{perc}\qquad\qquad t_{NY}=1 \,\mathrm{nap} + 4,87 \,\mathrm{perc}$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
<wlatex>#: a) Az órák nem fogják ugyanazt az időt mutatni. Ennek egyik oka az, hogy különböző szögsebességgel forgő vonatkoztatási rendszerben vannak nyugalomban, így más a rájuk ható tehetetlenségi erő nagysága. Másik ok származhat relativisztikus effektusokból, de ezekkel itt nem foglalkozunk. | <wlatex>#: a) Az órák nem fogják ugyanazt az időt mutatni. Ennek egyik oka az, hogy különböző szögsebességgel forgő vonatkoztatási rendszerben vannak nyugalomban, így más a rájuk ható tehetetlenségi erő nagysága. Másik ok származhat relativisztikus effektusokból, de ezekkel itt nem foglalkozunk. | ||
A lap jelenlegi, 2014. január 9., 15:32-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*4.24) Az Egyenlítőn fekvő repülőtéren három teljesen egyforma ingaóra van. Az
ingaóra a repülőtéren marad, a 
ingaórát egy kelet, a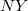 
-t egy nyugat felé induló repülőgépre helyezik. Pontosan délben - amikor mindhárom óra ugyanazt az időt mutatja - a repülőgépek elindulnak és egyenletes sebességgel körberepülik a Földet, úgy, hogy egyszerre érjenek vissza a kiindulási repülőtérre. Visszaérkezésükkor az óra éppen következő nap déli 12 óra 0 perc 0 másodpercet mutat.
- a) Mindhárom óra ugyanezt az időt mutatja-e? Ha nem, soroljunk fel különböző okokat, melyek az időkülönbséget előidézhetik!
- b) A legjelentősebb hatás figyelembevételével adjuk meg, hogy mennyivel fog többet, illetve kevesebbet mutatni a , illetve az 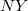óra a 24 órás repülés után!
Megoldás
- a) Az órák nem fogják ugyanazt az időt mutatni. Ennek egyik oka az, hogy különböző szögsebességgel forgő vonatkoztatási rendszerben vannak nyugalomban, így más a rájuk ható tehetetlenségi erő nagysága. Másik ok származhat relativisztikus effektusokból, de ezekkel itt nem foglalkozunk.
- b) Mindegyik inga forgó vonatkoztatási rendszerben van nyugalomban. A vonatkoztatási rendszerek forgása nem gyorsuló, ezért csak a centrifugális és Coriolis erők léphetnek fel. A Föld nagy
sugara miatt a centrifugális erő nagysága ahol![\[F_{cf}=m\omega^{2}R\,,\]](/images/math/4/4/a/44a7f37c96b8843d66bdb1369927cd09.png)
a vonatkoztatási rendszer forgásának szögsebessége és 
az ingák tömege. A centrifugális erő a Föld középpontjától kifelé mutat.
A Coriolis erő nagysága és iránya függ a lengés irányától, azonban a Coriolis-erő a sebességnek csak az irányát változtatja meg, így nem várhatjuk, hogy első rendben befolyásolná a lengés időt.
A centrifugális erő figyelembevételével az ingára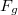
helyett egy 
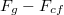erő hat. Tehát tekinthetünk úgy a szituárcióra, mintha egy nyugalomban lévő inga esetében a gravitációs gyorsulás 
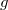helyett 
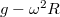lenne. Így az inga lengésideje 
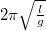helyett ahol hangsúlyozzuk, hogy![\[T(\omega)=2\pi\sqrt{\frac{l}{g-\omega^{2}R}}\,,\]](/images/math/3/1/6/316345c8a1205ae169f72424f3a1d274.png)
nem az inga jellemzője, hanem a vonatkoztatási rendszer forgásának szögsebessége. A különböző ingaórák esetében ez a szögsebesség ahol![\[\omega_{A}=\frac{2\pi}{t_{day}}\qquad \omega_{K}=2\frac{2\pi}{1\,\mathrm{nap}}=2\omega_{A}\qquad\omega_{NY}=0\,,\]](/images/math/e/1/f/e1ffe5f874f0b73979e04e531ae28bda.png)
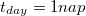. A Föld adataival jóval kisebb, mint![\[\omega_{A}^{2}R=0,03373\,\mathrm{\frac{m}{s^{2}}}\]](/images/math/8/c/8/8c8fb74f73a4643ef574ddeddf9471bb.png)
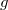. A inga esetén is kicsi ez a mennyiség. Az ingák lengésideje Az![\[T_{A}=2\pi\sqrt{\frac{l}{g-\omega_{A}^{2}R}}\qquad T_{K}=2\pi\sqrt{\frac{l}{g-4\omega_{A}^{2}R}}\qquad T_{NY}=2\pi\sqrt{\frac{l}{g}}\]](/images/math/d/f/c/dfc122fdc59d2a7dc68844f3052fc0b7.png)
ingaórán mért idő 
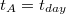. A és 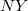ingaórákon mért idő pedig és![\[t_{K}=t_{day}\frac{T_{A}}{T_{K}}=t_{day}\sqrt{\frac{g-4\omega_{A}^{2}R}{g-\omega_{A}^{2}R}}=0,995\cdot t_{day}=1 \,\mathrm{nap} - 7,33 \,\mathrm{perc} \]](/images/math/0/4/1/0410aa6b33d4491b7c01b3a7ad69049e.png)
![\[t_{NY}=t_{day}\frac{T_{A}}{T_{NY}}=t_{day}\sqrt{\frac{g}{g-\omega_{A}^{2}R}}=1,0017\cdot t_{day}=1 \,\mathrm{nap} + 4,87 \,\mathrm{perc} \,.\]](/images/math/3/6/5/3650ce3ba50081b75facdf2b1a727f79.png)
