„Mechanika - Rezgő merev rúd feszültségállapota” változatai közötti eltérés
A Fizipedia wikiből
(→Megoldás) |
|||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
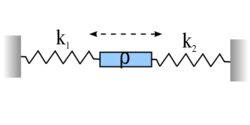
| − | </noinclude><wlatex># (5.15.) | + | </noinclude><wlatex># (*5.15.) Egy $\rho$ sűrűségű, $A$ keresztmetszetű és $l$ hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben, és egyensúlyi helyzetében mindkét rugó nyújtatlan. Bizonyítsuk be, hogy a mechanikai feszültség a rúd mentén egyenletesen változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?[[Kép:Kfgy1-5-15.svg|none|250px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a Newton-féle mozgásegyenletet a rúd egy kis $dx$ hosszúságú darabjára!}}{{Végeredmény|content=Mivel a test merev, a gyorsulás független a helytől, ezért a mechanikai feszültség csak lineárisan változhat. A rúd végein a feszültség és a keresztmetszet szorzata egyenlő kell legyen az (időfüggő!) rugóerőkkel.}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
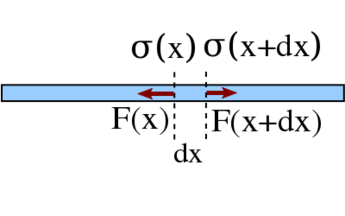
| − | <wlatex>A rúd egy tetszőleges kis $dx$ hosszúságú darabjának mozgásegyenlete $$a(x,t)dm=a(x)\rho Adx= | + | <wlatex> [[Kép:Kfgy1-5-15M2.svg|none|345px]] A rúd egy tetszőleges kis $dx$ hosszúságú darabjának mozgásegyenlete $$a(x,t)dm=a(x,t)\rho Adx=\sigma(x+dx,t)A-\sigma(x,t)A=d\sigma A=F(x+dx,t)+F(x,t),$$ ahol a két erő azonos előjelű feszültségek esetén ellentétes előjelű, mivel a darabka két oldalán hatnak. (Habár a modellünk merev test, ezek az erők a valóságban rugalmas eredetűek.) Ebből $A$-val egyszerűsítve és $dx$-el "átosztva" a $$\rho a(x,t)=\frac{d\sigma(x,t)}{dx}$$ egyenletet kapjuk. Mivel a rúd merev, a gyorsulása helyfüggetlen, így $a(x,t)=a(t)$, a deformáció mindenhol nulla (a Young modulus ebben a közelítésben végtelen, ahogy a rugalmas hullám terjedési sebessége is), a mechanikai feszültség viszont véges, és ugyanolyan jelleggel rezeg időben, ahogy a rúd kitérése és a vele arányos gyorsulása is. Továbbá a hely függvényében a feszültség csak lineáris lehet a gyorsulás hely szerint állandósága miatt. A $\sigma(x,t)$ függvény $x$ változó szerinti meredeksége időben folyamatosan változik, rezeg. Ha a rudat $\Delta x$ mértékben kimozdítjuk az egyensúlyi helyzetéből, az egyik rugó összenyomódik, a másik megnyúlik, így a rúd egyik vége nyomott, a másik húzott állapotban lesz, azaz a mechanika feszültség a rúd végein ellentétes előjelű, és az erősebb rugónál abszolút értékben nagyobb. Valahol a rúd mentén tehát a feszültség szükségképpen nulla, és ez nem feltétlenül a rúd közepén van, hanem a rúd hosszát a rugóállandók arányában kell felosztani. Ezen a helyen a feszültség viszont minden időpontban nulla! A feszültség a szélső értékeit végeredményben a rúd végein veszi fel. [[Kép:Kfgy1-5-15M.svg|none|350px]]</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. január 13., 16:54-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*5.15.) Egy
 sűrűségű,
sűrűségű,  keresztmetszetű és
keresztmetszetű és  hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben, és egyensúlyi helyzetében mindkét rugó nyújtatlan. Bizonyítsuk be, hogy a mechanikai feszültség a rúd mentén egyenletesen változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?
hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben, és egyensúlyi helyzetében mindkét rugó nyújtatlan. Bizonyítsuk be, hogy a mechanikai feszültség a rúd mentén egyenletesen változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?
Megoldás
A rúd egy tetszőleges kis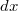 hosszúságú darabjának mozgásegyenlete
hosszúságú darabjának mozgásegyenlete ![\[a(x,t)dm=a(x,t)\rho Adx=\sigma(x+dx,t)A-\sigma(x,t)A=d\sigma A=F(x+dx,t)+F(x,t),\]](/images/math/8/5/4/8545bfaed3c0dde1c34df2a4134ed9cc.png)
 -val egyszerűsítve és
-val egyszerűsítve és 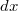 -el "átosztva" a
-el "átosztva" a ![\[\rho a(x,t)=\frac{d\sigma(x,t)}{dx}\]](/images/math/b/4/3/b4391124e0ed24a0d93fe01300fdf107.png)
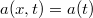 , a deformáció mindenhol nulla (a Young modulus ebben a közelítésben végtelen, ahogy a rugalmas hullám terjedési sebessége is), a mechanikai feszültség viszont véges, és ugyanolyan jelleggel rezeg időben, ahogy a rúd kitérése és a vele arányos gyorsulása is. Továbbá a hely függvényében a feszültség csak lineáris lehet a gyorsulás hely szerint állandósága miatt. A
, a deformáció mindenhol nulla (a Young modulus ebben a közelítésben végtelen, ahogy a rugalmas hullám terjedési sebessége is), a mechanikai feszültség viszont véges, és ugyanolyan jelleggel rezeg időben, ahogy a rúd kitérése és a vele arányos gyorsulása is. Továbbá a hely függvényében a feszültség csak lineáris lehet a gyorsulás hely szerint állandósága miatt. A 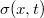 függvény
függvény  változó szerinti meredeksége időben folyamatosan változik, rezeg. Ha a rudat
változó szerinti meredeksége időben folyamatosan változik, rezeg. Ha a rudat 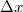 mértékben kimozdítjuk az egyensúlyi helyzetéből, az egyik rugó összenyomódik, a másik megnyúlik, így a rúd egyik vége nyomott, a másik húzott állapotban lesz, azaz a mechanika feszültség a rúd végein ellentétes előjelű, és az erősebb rugónál abszolút értékben nagyobb. Valahol a rúd mentén tehát a feszültség szükségképpen nulla, és ez nem feltétlenül a rúd közepén van, hanem a rúd hosszát a rugóállandók arányában kell felosztani. Ezen a helyen a feszültség viszont minden időpontban nulla! A feszültség a szélső értékeit végeredményben a rúd végein veszi fel.
mértékben kimozdítjuk az egyensúlyi helyzetéből, az egyik rugó összenyomódik, a másik megnyúlik, így a rúd egyik vége nyomott, a másik húzott állapotban lesz, azaz a mechanika feszültség a rúd végein ellentétes előjelű, és az erősebb rugónál abszolút értékben nagyobb. Valahol a rúd mentén tehát a feszültség szükségképpen nulla, és ez nem feltétlenül a rúd közepén van, hanem a rúd hosszát a rugóállandók arányában kell felosztani. Ezen a helyen a feszültség viszont minden időpontban nulla! A feszültség a szélső értékeit végeredményben a rúd végein veszi fel.