„Deriválás - Szélsőértékek” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
<noinclude> | <noinclude> | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
| − | [[Kategória:Szerkesztő: | + | [[Kategória:Szerkesztő: Bácsi Ádám]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| 7. sor: | 7. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex> | + | </noinclude><wlatex># Tekintsük az alábbi, valós számokon értelmezett függvényt: |
| − | # Tekintsük az alábbi, valós számokon értelmezett függvényt: | + | |
#: $$f(x) = 2 x^3 - 3 x^2 - 36 x + 12$$ | #: $$f(x) = 2 x^3 - 3 x^2 - 36 x + 12$$ | ||
#: Hol vannak a függvény lokalás szélsőértékei, és azok milyenek?</wlatex><includeonly></includeonly><noinclude> | #: Hol vannak a függvény lokalás szélsőértékei, és azok milyenek?</wlatex><includeonly></includeonly><noinclude> | ||
A lap jelenlegi, 2014. szeptember 9., 11:16-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Deriválás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Tekintsük az alábbi, valós számokon értelmezett függvényt:
-
![\[f(x) = 2 x^3 - 3 x^2 - 36 x + 12\]](/images/math/8/9/8/898466a504296a359d9d243e54859e42.png)
- Hol vannak a függvény lokalás szélsőértékei, és azok milyenek?
-
Megoldás
- Határozzuk meg a függvény első deriváltját!
-
![\[f'(x) = 6 x^2 - 6 x - 36\]](/images/math/8/5/6/856a05accb8d6d96aedc637c18c1c338.png)
- Egy lokális szélsőértéknél ez nulla kell legyen. Megoldva a másodfokú egyenletet:
-
![\[ x_{1,2} = \frac{6 \pm \sqrt{36 + 4 \cdot 36 \cdot 6}}{12} = \lbrace-2,\; +3 \rbrace\]](/images/math/e/8/5/e85c6d9b27f8c6a2aaa35d3eb98f2297.png)
- Határozzuk meg a második deriváltat!
-
![\[f''(x) = 12 x - 6\]](/images/math/9/f/3/9f385da1f6cba16aebc5f5f17f8d7b83.png)
- Ez az
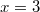-nál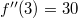 
, pozitív, azaz itt lokális minimuma van a függvénynek.
- Az
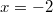pontban a második derivált értéke 
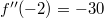, negatív, itt lokális maximuma van a függvénynek.
