„Erőtan II. - Forgó rotor még egyszer” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám Kategória:Mechanika - Erőtan II. {{Kísérleti fizika gyakorl…”) |
(→Feladat) |
||
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># | + | </noinclude><wlatex># Oldjuk meg az [[Erőtan I. - 2.4.4|Erőtan I. - 2.4.4]] feladatot újból, de most a rotorral együttforgó koordinátarendszerben! Ha $l \omega^2 > g$, adjuk meg az inga rezgéseinek frekvenciáját, ha kicsit kitérítjük egyensúlyi helyzetéből. (Tegyük fel, hogy az ingát a rotorhoz egy merev rúd köti, ami a rotorral együtt forog.) </wlatex><includeonly><wlatex>{{Végeredmény|content= Lásd a teljes megoldást!}}</wlatex></includeonly><noinclude> |
| − | Oldjuk meg az [[Erőtan I. - 2.4.4|Erőtan I. - 2.4.4]] feladatot újból, de most a rotorral együttforgó koordinátarendszerben! Ha $l \omega^2 > g$, adjuk meg az inga rezgéseinek frekvenciáját, ha | + | |
| − | kicsit kitérítjük egyensúlyi helyzetéből. (Tegyük fel, hogy az ingát a rotorhoz egy merev rúd köti, ami a rotorral együtt forog.) | + | |
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content= | + | |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: | + | <wlatex>#: Ha az inga szögkitérése $\varphi$, úgy rá vízszintesen $F_{cf} = m L \sin(\varphi) \omega^2$ centrifugális erő hat a forgó k.r. -ben. Ennek a tangenciális komponense $m L \omega^2 \sin(\varphi) \cos(\varphi)$. A nehézségi erő tangenciális komponense $- m g \sin(\varphi)$. Az egyensúly feltétele tangenciális irányban: $$ m L \omega^2 \sin(\varphi) \cos(\varphi) - m g \sin(\varphi) = 0 \; .$$ Ennek az egyenletnek triviális megoldása a $\varphi = 0$. Ha azonban véges kitérése van, úgy $$L \omega^2 \cos(\varphi) = g \; ,$$ amiből $\cos(\varphi) = \frac{g}{L \omega^2}$. Ez csak akkor ad megoldást, ha a jobboldal kisebb 1-nél, azaz $L \omega^2 > g$. |
| + | #: Írjuk fel az inga mozgásegyenletét tetszőleges kitérés esetén. Ha a rotor nem engedi kicsavarodni az ingát, úgy a Coriolis erőt a rotor kompenzálja, ezért csak a centrifugális erővel kell számolni. A tangenciális mozgásegyenlet: $$m L \ddot{\varphi} = m L \omega^2 \sin(\varphi) \cos(\varphi) - m g \sin(\varphi) \; , $$ azaz $$\ddot{\varphi} = \omega^2 \sin(\varphi) \cos(\varphi) - \frac{g}{L} \sin(\varphi) \; .$$ Fejtsük lineáris rendig Taylor sorba ezt a kifejezést $\varphi_0 = \arccos \left( \frac{ g}{L \omega^2} \right)$ körül. Mivel $\varphi_0$ épp az egyensúlyi helyzet, a konstans tag eltűnik. A jobboldal első deriváltja: $$\omega^2 (\cos^2(\varphi) - \sin^2(\varphi)) - \frac{g}{L} \cos(\varphi) = \omega^2 (2 \cos^2(\varphi) - 1) - \frac{g}{L} \cos(\varphi)\; . $$ Behelyettesítve ebbe $\varphi_0$ értékét: $$\omega^2 \left(2 \frac{g^2}{L^2 \omega^4} - 1 \right) - \frac{g^2}{L^2 \omega^2} = \frac{g^2}{L^2 \omega^2} - \omega^2 \; .$$ Ezzel a $\varphi_0$ körüli kis kitérések esetén: $$\ddot{\varphi} \approx - \left( \omega^2 - \frac{g^2}{L^2 \omega^2} \right) (\varphi - \varphi_0) \; .$$ A rezgések körfrekvenciája innen leolvasva: $$\Omega = \sqrt{ \omega^2 - \frac{g^2}{L^2 \omega^2}} \; . $$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. november 10., 21:04-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Oldjuk meg az Erőtan I. - 2.4.4 feladatot újból, de most a rotorral együttforgó koordinátarendszerben! Ha
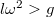, adjuk meg az inga rezgéseinek frekvenciáját, ha kicsit kitérítjük egyensúlyi helyzetéből. (Tegyük fel, hogy az ingát a rotorhoz egy merev rúd köti, ami a rotorral együtt forog.)
Megoldás
- Ha az inga szögkitérése
, úgy rá vízszintesen 
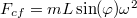centrifugális erő hat a forgó k.r. -ben. Ennek a tangenciális komponense 
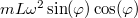. A nehézségi erő tangenciális komponense 
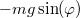. Az egyensúly feltétele tangenciális irányban: Ennek az egyenletnek triviális megoldása a![\[ m L \omega^2 \sin(\varphi) \cos(\varphi) - m g \sin(\varphi) = 0 \; .\]](/images/math/2/5/0/25011c4c0a6afea2c0bbdeef3eaac174.png)
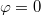. Ha azonban véges kitérése van, úgy amiből![\[L \omega^2 \cos(\varphi) = g \; ,\]](/images/math/1/6/e/16ea6376add4728afef7bcd4b4d80310.png)
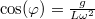. Ez csak akkor ad megoldást, ha a jobboldal kisebb 1-nél, azaz 
.
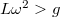- Írjuk fel az inga mozgásegyenletét tetszőleges kitérés esetén. Ha a rotor nem engedi kicsavarodni az ingát, úgy a Coriolis erőt a rotor kompenzálja, ezért csak a centrifugális erővel kell számolni. A tangenciális mozgásegyenlet: azaz
![\[m L \ddot{\varphi} = m L \omega^2 \sin(\varphi) \cos(\varphi) - m g \sin(\varphi) \; , \]](/images/math/d/7/4/d7412d01aaa6b0e75bd1558f1a867669.png)
Fejtsük lineáris rendig Taylor sorba ezt a kifejezést![\[\ddot{\varphi} = \omega^2 \sin(\varphi) \cos(\varphi) - \frac{g}{L} \sin(\varphi) \; .\]](/images/math/7/9/c/79c05c385def5063c59a16bab91afa76.png)
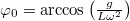körül. Mivel 
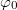épp az egyensúlyi helyzet, a konstans tag eltűnik. A jobboldal első deriváltja: Behelyettesítve ebbe![\[\omega^2 (\cos^2(\varphi) - \sin^2(\varphi)) - \frac{g}{L} \cos(\varphi) = \omega^2 (2 \cos^2(\varphi) - 1) - \frac{g}{L} \cos(\varphi)\; . \]](/images/math/4/e/b/4eb1542881f94bbf23ab829a74a2be64.png)
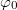értékét: Ezzel a![\[\omega^2 \left(2 \frac{g^2}{L^2 \omega^4} - 1 \right) - \frac{g^2}{L^2 \omega^2} = \frac{g^2}{L^2 \omega^2} - \omega^2 \; .\]](/images/math/0/2/0/0200ca9ebb1bc5df2549c00e8c18f931.png)
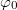körüli kis kitérések esetén: A rezgések körfrekvenciája innen leolvasva:![\[\ddot{\varphi} \approx - \left( \omega^2 - \frac{g^2}{L^2 \omega^2} \right) (\varphi - \varphi_0) \; .\]](/images/math/b/5/1/b5167a49689328282a21e0759067c6cf.png)
![\[\Omega = \sqrt{ \omega^2 - \frac{g^2}{L^2 \omega^2}} \; . \]](/images/math/c/4/5/c45f2da92140ab06fbd5ebb43c4809db.png)
- Ha az inga szögkitérése
