„Mechanika - Fémhuzal önsúllyal” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
a |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># (5.2.) Egy erőmentes állapotban $l_0$ hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége $\rho$, Young-modulusa $E$, egyenletes keresztmetszete pedig $A$. | + | </noinclude><wlatex># (*5.2.) Egy erőmentes állapotban $l_0$ hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége $\rho$, Young-modulusa $E$, egyenletes keresztmetszete pedig $A$. |
#: a) Mennyivel változik meg a huzal hossza? | #: a) Mennyivel változik meg a huzal hossza? | ||
#: b) Mennyi lesz a megnyúlás, ha a huzal alsó végére egy m tömegű testet akasztunk?</wlatex><includeonly><wlatex>{{Útmutatás|content=A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel.}}{{Végeredmény|content=$$\Delta l=\frac{\rho l_0^2g}{2E}$$ $$\Delta l_2=\Delta l+\frac{mg}{EA}l_0$$}}</wlatex></includeonly><noinclude> | #: b) Mennyi lesz a megnyúlás, ha a huzal alsó végére egy m tömegű testet akasztunk?</wlatex><includeonly><wlatex>{{Útmutatás|content=A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel.}}{{Végeredmény|content=$$\Delta l=\frac{\rho l_0^2g}{2E}$$ $$\Delta l_2=\Delta l+\frac{mg}{EA}l_0$$}}</wlatex></includeonly><noinclude> | ||
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A huzal hosszváltozását az önsúlya idézi elő lelógatott állapotában. Feltesszük, hogy a $g$ nehézségi gyorulás a huzal mentén állandó. A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel. A kis szakaszok (relatív) megnyúlása a huzal mentén változik a szintén változó feszültségi állapot miatt. A huzal aljától $x$ távolságra található $\text{d}x$ hosszúságú szakasz feszültsége $\sigma(x)=\rho x g,$ amely a Hooke-törvény szerint $E\frac{\Delta(\text{d}x}{\text{d}x}$-vel is egyenlő, ahol a számláló a kis szakasz megnyúlása. Ezt kifejezve $\Delta(\text{d}x)=\frac{\rho x g}E \text{d}x$, mely a huzal teljes (eredeti) hosszára integrálva adja a teljes megnyúlást: $$\Delta l=\int_0^{l_0}\Delta(\text{d}x)=\int_0^{l_0}\frac{\rho x g}E\text{d}x=\frac{\rho l_0^2g}{2E}$$ Ha további $m$ tömeget akasztunk a huzal végére, a feszültség kifejezésében egy plusz $\frac{mg}A$ tag jelenik meg, így végül a teljes megnyúlás $$\Delta l_2=\Delta l+\frac{mg}{EA}l_0$$</wlatex> | + | <wlatex>A huzal hosszváltozását az önsúlya idézi elő lelógatott állapotában. Feltesszük, hogy a $g$ nehézségi gyorulás a huzal mentén állandó. A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel. A kis szakaszok (relatív) megnyúlása a huzal mentén változik a szintén változó feszültségi állapot miatt. A huzal aljától $x$ távolságra található $\text{d}x$ hosszúságú szakasz feszültsége $\sigma(x)=\rho x g,$ amely a Hooke-törvény szerint $E\frac{\Delta(\text{d}x)}{\text{d}x}$-vel is egyenlő, ahol a számláló a kis szakasz megnyúlása. Ezt kifejezve $\Delta(\text{d}x)=\frac{\rho x g}E \text{d}x$, mely a huzal teljes (eredeti) hosszára integrálva adja a teljes megnyúlást: $$\Delta l=\int_0^{l_0}\Delta(\text{d}x)=\int_0^{l_0}\frac{\rho x g}E\text{d}x=\frac{\rho l_0^2g}{2E}$$ Ha további $m$ tömeget akasztunk a huzal végére, a feszültség kifejezésében egy plusz $\frac{mg}A$ tag jelenik meg, így végül a teljes megnyúlás $$\Delta l_2=\Delta l+\frac{mg}{EA}l_0$$</wlatex> |
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2015. november 11., 13:00-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (*5.2.) Egy erőmentes állapotban
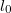 hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége
hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége  , Young-modulusa
, Young-modulusa  , egyenletes keresztmetszete pedig
, egyenletes keresztmetszete pedig  .
.
- a) Mennyivel változik meg a huzal hossza?
- b) Mennyi lesz a megnyúlás, ha a huzal alsó végére egy m tömegű testet akasztunk?
Megoldás
A huzal hosszváltozását az önsúlya idézi elő lelógatott állapotában. Feltesszük, hogy a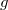 nehézségi gyorulás a huzal mentén állandó. A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel. A kis szakaszok (relatív) megnyúlása a huzal mentén változik a szintén változó feszültségi állapot miatt. A huzal aljától
nehézségi gyorulás a huzal mentén állandó. A teljes hosszváltozást úgy kaphatjuk meg, hogy a huzal kis szakaszainak hosszváltozását összegezzük fel. A kis szakaszok (relatív) megnyúlása a huzal mentén változik a szintén változó feszültségi állapot miatt. A huzal aljától  távolságra található
távolságra található 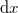 hosszúságú szakasz feszültsége
hosszúságú szakasz feszültsége 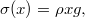 amely a Hooke-törvény szerint
amely a Hooke-törvény szerint 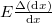 -vel is egyenlő, ahol a számláló a kis szakasz megnyúlása. Ezt kifejezve
-vel is egyenlő, ahol a számláló a kis szakasz megnyúlása. Ezt kifejezve 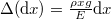 , mely a huzal teljes (eredeti) hosszára integrálva adja a teljes megnyúlást:
, mely a huzal teljes (eredeti) hosszára integrálva adja a teljes megnyúlást: ![\[\Delta l=\int_0^{l_0}\Delta(\text{d}x)=\int_0^{l_0}\frac{\rho x g}E\text{d}x=\frac{\rho l_0^2g}{2E}\]](/images/math/c/0/b/c0b59b9f20f209400efc8430a183c00f.png)
 tömeget akasztunk a huzal végére, a feszültség kifejezésében egy plusz
tömeget akasztunk a huzal végére, a feszültség kifejezésében egy plusz 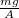 tag jelenik meg, így végül a teljes megnyúlás
tag jelenik meg, így végül a teljes megnyúlás ![\[\Delta l_2=\Delta l+\frac{mg}{EA}l_0\]](/images/math/3/7/e/37e7e530bb9d799f575d73019534bd66.png)