„Deriválás” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Bácsi Ádám {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gyakorlat 1. | …”)
 
 
(2 szerkesztő 4 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
−
[[Kategória:Szerkesztő:Bácsi Ádám]]
+
[[Kategória:Szerkesztő: Bácsi Ádám]]
 
{{Kísérleti fizika gyakorlat
 
{{Kísérleti fizika gyakorlat
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
13. sor: 13. sor:
 
{{:Deriválás - Inverz függvény deriváltja}}{{Megoldás|link=Deriválás - Inverz függvény deriváltja}}
 
{{:Deriválás - Inverz függvény deriváltja}}{{Megoldás|link=Deriválás - Inverz függvény deriváltja}}
 
{{:Deriválás - Hiperbolikus függvények}}{{Megoldás|link=Deriválás - Hiperbolikus függvények}}
 
{{:Deriválás - Hiperbolikus függvények}}{{Megoldás|link=Deriválás - Hiperbolikus függvények}}
 +
{{:Deriválás - Szélsőértékek}}{{Megoldás|link=Deriválás - Szélsőértékek}}
 +
{{:Deriválás - Egyváltozós vektorfüggvény}}{{Megoldás|link=Deriválás - Egyváltozós vektorfüggvény}}

A lap jelenlegi, 2014. szeptember 9., 13:23-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája:
  1. Deriválás
  2. Integrálás
  3. Mozgástan
  4. Erőtan I.
  5. Erőtan II.
  6. Munka, energia
  7. Pontrendszerek
  8. Merev testek I.
  9. Merev testek II.
  10. Rugalmasság, folyadékok
  11. Rezgések I.
  12. Rezgések II.
  13. Hullámok
Deriválás
Feladatok listája:
  1. Alapműveletek vektorokkal
  2. Vektorok felbontása
  3. Egyszerű deriváltak
  4. Inverz függvény deriváltja
  5. Hiperbolikus függvények
  6. Szélsőértékek
  7. Egyvátozós vektorfüggvény
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladatok


  1. Adottak az alábbi vektorok.
    \[\mathbf{v}_{1}=\left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]\qquad\qquad\mathbf{v}_{2}=\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\]
    a) Határozzuk meg az 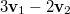\setbox0\hbox{$3\mathbf{v}_{1}-2\mathbf{v}_{2}$}% \message{//depth:\the\dp0//}% \box0% vektort!
    b) Mekkora a vektorok normája (nagysága)?
    c) Mekkora szöget zár be a két vektor?
    d) Adjuk meg a 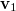\setbox0\hbox{$\mathbf{v}_{1}$}% \message{//depth:\the\dp0//}% \box0% vektor 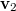\setbox0\hbox{$\mathbf{v}_{2}$}% \message{//depth:\the\dp0//}% \box0% irányába eső komponensét!
  2. Egy \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0% hajlásszögű lejtőn nyugszik egy \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegű test.
    a) Határozzuk a gravitációs erő lejtőre merőleges és lejtővel párhuzamos komponenseinek nagyságát!
    b) Adjuk meg a nyomóerő függőleges és vízszintes komponenseinek nagyságát!
  3. Határozzuk meg az alábbi függvények első deriváltját! Az f) feladatrészben a második deriváltat is számoljuk ki!
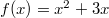
    a) \setbox0\hbox{$f(x)=x^{2}+3x$}% \message{//depth:\the\dp0//}% \box0%
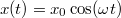
    b) \setbox0\hbox{$x(t)=x_{0}\cos(\omega t)$}% \message{//depth:\the\dp0//}% \box0%
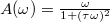
    c) \setbox0\hbox{$A(\omega)=\frac{\omega}{1+(\tau\omega)^{2}}$}% \message{//depth:\the\dp0//}% \box0%
    d) \setbox0\hbox{$h(x)=\sin\left[\ln\left(\cos(3x)\right)\right]$}% \message{//depth:\the\dp0//}% \box0%
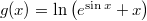
    e) \setbox0\hbox{$g(x)=\ln\left(e^{\sin x}+x\right)$}% \message{//depth:\the\dp0//}% \box0%
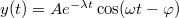
    f) \setbox0\hbox{$y(t)=Ae^{-\lambda t}\cos(\omega t-\varphi)$}% \message{//depth:\the\dp0//}% \box0%
  4. * Tegyük fel, hogy ismerjük egy 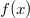\setbox0\hbox{$f(x)$}% \message{//depth:\the\dp0//}% \box0% függvény deriváltját. Ekkor az 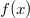\setbox0\hbox{$f(x)$}% \message{//depth:\the\dp0//}% \box0% függvény 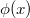\setbox0\hbox{$\phi(x)$}% \message{//depth:\the\dp0//}% \box0% inverzének deriváltja
    \[\frac{d\phi}{dx}=\frac{1}{f'(\phi(x))}\,.\]
    Ennek segítségével számítsuk ki az alábbi függvények deriváltját.
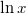
    a) \setbox0\hbox{$\mbox{ln}\,x$}% \message{//depth:\the\dp0//}% \box0%
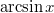
    b) \setbox0\hbox{$\mbox{arcsin}\,x$}% \message{//depth:\the\dp0//}% \box0%
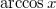
    c) \setbox0\hbox{$\mbox{arccos}\,x$}% \message{//depth:\the\dp0//}% \box0%
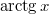
    d) \setbox0\hbox{$\mbox{arctg}\,x$}% \message{//depth:\the\dp0//}% \box0%
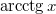
    e) \setbox0\hbox{$\mbox{arcctg}\,x$}% \message{//depth:\the\dp0//}% \box0%
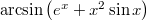
    f) \setbox0\hbox{$\mbox{arcsin}\left(e^{x}+x^{2}\sin x\right)$}% \message{//depth:\the\dp0//}% \box0%
    g) \setbox0\hbox{$\mbox{arctg}\,\left[2\ln x+\sin(\cos x)\right]$}% \message{//depth:\the\dp0//}% \box0%
  5. * A hiperbolikus függvényeket a következőképpen definiáljuk.
    \[\mbox{ch}\,x=\frac{e^{x}+e^{-x}}{2}\qquad\qquad \mbox{sh}\,x= \frac{e^{x}-e^{-x}}{2}\]
    \[ \mbox{th}\,x=\frac{\mbox{sh}\, x}{\mbox{ch}\, x}\qquad\qquad \mbox{cth}\,x=\frac{\mbox{ch}\,x}{\mbox{sh}\,x}\]
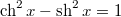    a) Igazoljuk, hogy \setbox0\hbox{$\mbox{ch}^{2}\,x-\mbox{sh}^{2}\,x=1$}% \message{//depth:\the\dp0//}% \box0%!
    b) Számoljuk ki a hiperbolikus függvények deriváltjait!
    c) Határozzuk meg a \setbox0\hbox{$\mbox{ch}\, x$}% \message{//depth:\the\dp0//}% \box0% függvény inverzét és annak deriváltját.
  6. Tekintsük az alábbi, valós számokon értelmezett függvényt:
    \[f(x) = 2 x^3 - 3 x^2 - 36 x + 12\]
    Hol vannak a függvény lokalás szélsőértékei, és azok milyenek?
  7. Tekintsük az alábbi, valós számokról a 3 dimenziós vektorok terébe képező függvényt!
    \[ \vec{v}(s) = \left( \begin{array}{c} \sin s \\ 2 \cos s \\ 3 s \end{array} \right) \]
    a) Határozzuk meg ennek a 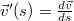\setbox0\hbox{$\vec{v}'(s) = \frac{d \vec{v}}{d s}$}% \message{//depth:\the\dp0//}% \box0% deriváltját!
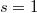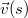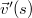    b) Mekkora szöget zárnak be az \setbox0\hbox{$s = 1$}% \message{//depth:\the\dp0//}% \box0% helyen a \setbox0\hbox{$\vec{v}(s)$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\vec{v}'(s)$}% \message{//depth:\the\dp0//}% \box0% vektorok?
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Deriválás&oldid=14903”