„Deriválás - Vektorok felbontása” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Bácsi Ádám {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika gya…”)
 
 
(egy szerkesztő 4 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
<noinclude>
 
<noinclude>
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
 
[[Kategória:Kísérleti fizika gyakorlat 1.]]
−
[[Kategória:Szerkesztő:Bácsi Ádám]]
+
[[Kategória:Szerkesztő: Bácsi Ádám]]
 
{{Kísérleti fizika gyakorlat
 
{{Kísérleti fizika gyakorlat
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
 
| tárgynév    = Kísérleti fizika gyakorlat 1.
7. sor: 7. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex>
+
</noinclude><wlatex># Egy $\alpha$ hajlásszögű lejtőn nyugszik egy $m$ tömegű test.
−
# Adottak az alábbi vektorok.
+
#: a) Határozzuk a gravitációs erő lejtőre merőleges és lejtővel párhuzamos komponenseinek nagyságát!
−
#: $$\mathbf{v}_{1}=\left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]\qquad\qquad\mathbf{v}_{2}=\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]$$
+
#: b) Adjuk meg a nyomóerő függőleges és vízszintes komponenseinek nagyságát!</wlatex><includeonly></includeonly><noinclude>
−
#: a) Határozzuk meg az $3\mathbf{v}_{1}-2\mathbf{v}_{2}$ vektort!
+
−
#: b) Mekkora a vektorok normája (nagysága)?
+
−
#: c) Mekkora szöget zár be a két vektor?
+
−
#: d) Adjuk meg a $\mathbf{v}_{1}$ vektor $\mathbf{v}_{2}$ irányába eső komponensét!
+
−
</wlatex>
+
−
<includeonly>
+
−
</includeonly>
+
−
<noinclude>
+
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>
+
<wlatex>#: a) A lejtőre merőleges komponens nagysága $F_{g1}=mg\cos\alpha$, amely $\alpha=0$ esetben természetesen visszaadja a teljes gravitációs erőt. <br> A lejtővel párhuzamos komponens $F_{g2}=mg\sin\alpha$, amely $\alpha=0$ esetben zérus.
−
#: a) $$ 3\mathbf{v}_{1}-2\mathbf{v}_{2}= 3 \left[\begin{array}{c} 1 \\ 2 \\ -1 \end{array}\right]-
+
#: b) A nyomóerő a lejtőre merőleges irányba mutat úgy, hogy a függőlegessel bezárt szöge $\alpha$. Így a függőleges komponensének nagysága $N_{1}=N\cos\alpha$, vízszintes komponensének nagysága pedig $N_{2}=N\sin\alpha$.</wlatex>
−
2 \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]= \left[\begin{array}{c} 3 \\ 6 \\ -3 \end{array}\right]-
+
−
\left[\begin{array}{c} 0 \\ 2 \\ 2 \end{array}\right]= \left[\begin{array}{c} 3 \\ 4 \\ -5 \end{array}\right]$$
+
−
#: b) $$|\mathbf{v}_{1}|^{2}=1^{2}+2^{2}+(-1)^{2}=6\qquad\Rightarrow\qquad |\mathbf{v}_{1}|=\sqrt{6}$$$$|\mathbf{v}_{2}|^{2}=0^{2}+1^{2}+1^{2}=2\qquad\Rightarrow\qquad |\mathbf{v}_{2}|=\sqrt{2}$$
+
−
#: c) Bármely két vektor esetén $$\mathbf{v}_{1}\cdot\mathbf{v}_{2}=|\mathbf{v}_{1}||\mathbf{v}_{2}|\cos\alpha\,,$$ ahol $\cdot$ a vektorok skaláris szorzását jelöli és $\alpha$ a két vektor által bezárt szög. Ebben a feladatban $$\mathbf{v}_{1}\cdot\mathbf{v}_{2}=1\cdot 0+ 2\cdot 1+ -1\cdot 1=1\,,$$ tehát $$1=\sqrt{6}\sqrt{2}\cos\alpha\qquad\Rightarrow\qquad \alpha=73,2\,^{\circ}$$
+
−
#: d) A $\mathbf{v}_{2}$ vektor irányába mutató egység vektor $$\mathbf{n}_{2}=\frac{\mathbf{v}_{2}}{|\mathbf{v}_{2}|}=\frac{1}{\sqrt{2}}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.$$ Ezzel az egységvektorral a $\mathbf{v}_{1}$ vektor $\mathbf{n}_{2}$ irányába mutató komponense $$\mathbf{v}_{12}=\mathbf{n}_{2}(\mathbf{n}_{2}\cdot\mathbf{v}_{1})=\frac{1}{2}\left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right]\,.$$
+
−
</wlatex>
+
 
</noinclude>
 
</noinclude>

A lap jelenlegi, 2013. szeptember 11., 08:34-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája:
  1. Deriválás
  2. Integrálás
  3. Mozgástan
  4. Erőtan I.
  5. Erőtan II.
  6. Munka, energia
  7. Pontrendszerek
  8. Merev testek I.
  9. Merev testek II.
  10. Rugalmasság, folyadékok
  11. Rezgések I.
  12. Rezgések II.
  13. Hullámok
Deriválás
Feladatok listája:
  1. Alapműveletek vektorokkal
  2. Vektorok felbontása
  3. Egyszerű deriváltak
  4. Inverz függvény deriváltja
  5. Hiperbolikus függvények
  6. Szélsőértékek
  7. Egyvátozós vektorfüggvény
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Egy \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0% hajlásszögű lejtőn nyugszik egy \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegű test.
    a) Határozzuk a gravitációs erő lejtőre merőleges és lejtővel párhuzamos komponenseinek nagyságát!
    b) Adjuk meg a nyomóerő függőleges és vízszintes komponenseinek nagyságát!

Megoldás

  1. a) A lejtőre merőleges komponens nagysága 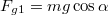\setbox0\hbox{$F_{g1}=mg\cos\alpha$}% \message{//depth:\the\dp0//}% \box0%, amely 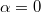\setbox0\hbox{$\alpha=0$}% \message{//depth:\the\dp0//}% \box0% esetben természetesen visszaadja a teljes gravitációs erőt.
    A lejtővel párhuzamos komponens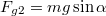 \setbox0\hbox{$F_{g2}=mg\sin\alpha$}% \message{//depth:\the\dp0//}% \box0%, amely 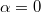\setbox0\hbox{$\alpha=0$}% \message{//depth:\the\dp0//}% \box0% esetben zérus.
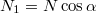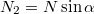    b) A nyomóerő a lejtőre merőleges irányba mutat úgy, hogy a függőlegessel bezárt szöge \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%. Így a függőleges komponensének nagysága \setbox0\hbox{$N_{1}=N\cos\alpha$}% \message{//depth:\the\dp0//}% \box0%, vízszintes komponensének nagysága pedig \setbox0\hbox{$N_{2}=N\sin\alpha$}% \message{//depth:\the\dp0//}% \box0%.
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Deriválás_-_Vektorok_felbontása&oldid=12075”