„Erőtan II. - 2.1.21” változatai közötti eltérés
A Fizipedia wikiből
| (2 szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
[[Kategória:Kísérleti fizika gyakorlat 1.]] | [[Kategória:Kísérleti fizika gyakorlat 1.]] | ||
[[Kategória:Szerkesztő: Bácsi Ádám]] | [[Kategória:Szerkesztő: Bácsi Ádám]] | ||
| − | [[Kategória:Erőtan | + | [[Kategória:Mechanika - Erőtan II.]] |
{{Kísérleti fizika gyakorlat | {{Kísérleti fizika gyakorlat | ||
| tárgynév = Kísérleti fizika gyakorlat 1. | | tárgynév = Kísérleti fizika gyakorlat 1. | ||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># Egy testre a nehézségi erőn kívül a sebességgel arányos fékező erő hat. ($F_{s}=-\alpha v$) | + | </noinclude><wlatex># (**2.1.21) Egy testre a nehézségi erőn kívül a sebességgel arányos fékező erő hat. ($F_{s}=-\alpha v$) |
#: a) Írjuk le a test mozgását, ha $h$ magasságból kezdősebesség nélkül indult! | #: a) Írjuk le a test mozgását, ha $h$ magasságból kezdősebesség nélkül indult! | ||
#: b) Milyen lesz a test mozgása $t\gg m/\alpha$ és $t\ll m/\alpha$ esetén? | #: b) Milyen lesz a test mozgása $t\gg m/\alpha$ és $t\ll m/\alpha$ esetén? | ||
#: c) Hogyan változik időben a test teljes energiája? | #: c) Hogyan változik időben a test teljes energiája? | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a mozgásegyenletet a függőleges mozgásra! Oldjuk meg az így kapott, sebességre vonatkozó differenciál egyenletet!}}{{Végeredmény|content= a) $$y(t)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)$$ <br> b) $$y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}$$ $$y\left(t\ | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a mozgásegyenletet a függőleges mozgásra! Oldjuk meg az így kapott, sebességre vonatkozó differenciál egyenletet!}}{{Végeredmény|content= a) $$y(t)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)$$ <br> b) $$y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}$$ $$y\left(t\ll \frac{m}{\alpha}\right)=h-\frac{g}{2}t^{2}$$ <br> c) $$E(t)=mg\left[h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\right]+\frac{g^{2}m^{3}}{2\alpha^{2}}\left(e^{-\frac{\alpha}{m}t}-1\right)^{2}$$}}</wlatex></includeonly><noinclude> |
| + | |||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>#: a) A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A mozgásegyenlet tehát $$ma=-mg-\alpha v$$ alakban írható. A gyorsulás a sebességnek az idő szerinti | + | <wlatex>#: a) A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A függőleges irányú mozgásegyenlet tehát $$ma=-mg-\alpha v$$ alakban írható. A mozgás az $y$ tengely mentén történik, amelyet úgy irányítunk, hogy a pozitív vége függőlegesen felfelé mutat. A gyorsulás a sebességnek az idő szerinti deriváltja, így a mozgásegyenlet matematikai szempontból egy elsőrendű, lineáris differenciálegyenlet a sebességre vonatkozóan. $$\dot{v}=-g-\frac{\alpha}{m}v$$ A differenciálegyenletet kell $v(0)=0$ kezdő feltétel mellett megoldani. $$\dot{v}=-\frac{\alpha}{m}\left(v+\frac{gm}{\alpha}\right)$$ Legyen $\tilde{v}(t)=v(t)+\frac{gm}{\alpha}$! Ezzel $$\dot{\tilde{v}}=-\frac{\alpha}{m}\tilde{v}\,,$$ melynek megoldása $$\tilde{v}(t)=Ae^{-\frac{\alpha}{m}t}$$ tetszőleges $A$ konstanssal, melyet majd a kezdeti feltétel segítségével tudunk meghatározni. $$v(t)=Ae^{-\frac{\alpha}{m}t}-\frac{gm}{\alpha}$$ A kezdeti feltétel $v(0)=0$. Ez csak úgy tud teljesülni, ha $$A=\frac{gm}{\alpha}\,.$$ Így a test sebessége az idő függvényében $$v(t)=\frac{gm}{\alpha}\left(e^{-\frac{\alpha}{m}t}-1\right)\,,$$ a test helyzete pedig az $y(0)=h$ kezdeti feltétellel $$y(t)=y(0)+\int_{0}^{t}v(t')dt'=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\,.$$ |
| − | #: b) Ha $t\gg \frac{m}{\alpha}$, akkor az exponenciálisok nagyon kicsivé válnak. $$v\left(t\gg \frac{m}{\alpha}\right)=-\frac{gm}{\alpha}$$ $$y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}$$ Elegendően sokat várva tehát már egyenes vonalú egyenletes mozgást végez a test. Ha $t\ll \frac{m}{\alpha}$, akkor az exponenciálisok argumentumában egy kis szám szerepel. Kihasználva azt a közelítést, miszerint kis $x$-re $e^{x}\approx 1+x$, megadhatunk egy közelítő formulát a sebességre. $$v\left(t\ | + | #: b) Ha $t\gg \frac{m}{\alpha}$, akkor az exponenciálisok nagyon kicsivé válnak. $$v\left(t\gg \frac{m}{\alpha}\right)=-\frac{gm}{\alpha}$$ $$y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}$$ Elegendően sokat várva tehát már egyenes vonalú egyenletes mozgást végez a test. Ha $t\ll \frac{m}{\alpha}$, akkor az exponenciálisok argumentumában egy kis szám szerepel. Kihasználva azt a közelítést, miszerint kis $x$-re $e^{x}\approx 1+x$, megadhatunk egy közelítő formulát a sebességre. $$v\left(t\ll \frac{m}{\alpha}\right)\approx \frac{gm}{\alpha}\left(1-\frac{\alpha}{m}t-1\right)= -gt$$ Az elmozdulás az ilyen rendű közelítésben csak $y(t)=h$ lenne. A közelítés következő rendjében $e^{x}\approx 1+x+\frac{x^{2}}{2}$, amely szerint $$y\left(t\ll \frac{m}{\alpha}\right)\approx h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1+\frac{\alpha}{m}t-\frac{1}{2}\left(\frac{\alpha}{m}t\right)^{2}\right)=h-\frac{g}{2}t^{2}\,.$$ Kis időkre tehát úgy viselkedik a test, mintha nem is hatna rá közegellenállás. Ez érthető is, hiszen ebben az idő tartományban még nagyon kicsi a sebesség és így kicsi a vele arányos közegellenállási erő. |
#: c) A test teljes energiája $$E(t)=mgy(t)+\frac{1}{2}mv(t)^{2}=mg\left[h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\right]+\frac{g^{2}m^{3}}{2\alpha^{2}}\left(e^{-\frac{\alpha}{m}t}-1\right)^{2}$$ szerint változik az időben. | #: c) A test teljes energiája $$E(t)=mgy(t)+\frac{1}{2}mv(t)^{2}=mg\left[h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\right]+\frac{g^{2}m^{3}}{2\alpha^{2}}\left(e^{-\frac{\alpha}{m}t}-1\right)^{2}$$ szerint változik az időben. | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2014. október 7., 14:07-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**2.1.21) Egy testre a nehézségi erőn kívül a sebességgel arányos fékező erő hat. (
)
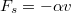- a) Írjuk le a test mozgását, ha
magasságból kezdősebesség nélkül indult!
- b) Milyen lesz a test mozgása
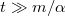és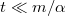 
esetén?
- c) Hogyan változik időben a test teljes energiája?
- a) Írjuk le a test mozgását, ha
Megoldás
- a) A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A függőleges irányú mozgásegyenlet tehát alakban írható. A mozgás az
![\[ma=-mg-\alpha v\]](/images/math/b/0/2/b02fba214baf6269ddbe92afd8dd9ed9.png)
tengely mentén történik, amelyet úgy irányítunk, hogy a pozitív vége függőlegesen felfelé mutat. A gyorsulás a sebességnek az idő szerinti deriváltja, így a mozgásegyenlet matematikai szempontból egy elsőrendű, lineáris differenciálegyenlet a sebességre vonatkozóan. A differenciálegyenletet kell![\[\dot{v}=-g-\frac{\alpha}{m}v\]](/images/math/5/6/3/5639e756b60091f74353ec12fc6a97e1.png)
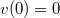kezdő feltétel mellett megoldani. Legyen![\[\dot{v}=-\frac{\alpha}{m}\left(v+\frac{gm}{\alpha}\right)\]](/images/math/7/2/d/72d34649338c773019a822645c927335.png)
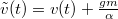! Ezzel melynek megoldása![\[\dot{\tilde{v}}=-\frac{\alpha}{m}\tilde{v}\,,\]](/images/math/8/8/c/88c95a70109f2495fb3db1172f8e0bb7.png)
tetszőleges![\[\tilde{v}(t)=Ae^{-\frac{\alpha}{m}t}\]](/images/math/a/9/a/a9af0d2bf7dc14ae98ff65107edaf491.png)
konstanssal, melyet majd a kezdeti feltétel segítségével tudunk meghatározni. A kezdeti feltétel![\[v(t)=Ae^{-\frac{\alpha}{m}t}-\frac{gm}{\alpha}\]](/images/math/b/f/b/bfb597278311c3a3cd29af7362cc13aa.png)
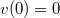. Ez csak úgy tud teljesülni, ha Így a test sebessége az idő függvényében![\[A=\frac{gm}{\alpha}\,.\]](/images/math/b/5/4/b545a601a2e5b9cec522585d3e8df9e2.png)
a test helyzete pedig az![\[v(t)=\frac{gm}{\alpha}\left(e^{-\frac{\alpha}{m}t}-1\right)\,,\]](/images/math/4/1/b/41be1c91079531721d3031e6ff8c0ad8.png)
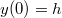kezdeti feltétellel ![\[y(t)=y(0)+\int_{0}^{t}v(t')dt'=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\,.\]](/images/math/e/d/c/edc5fec84ee26faf2849563f1802534a.png)
- b) Ha
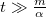, akkor az exponenciálisok nagyon kicsivé válnak. ![\[v\left(t\gg \frac{m}{\alpha}\right)=-\frac{gm}{\alpha}\]](/images/math/6/4/f/64f166ca4ae5a896d749e9a490280a7d.png)
Elegendően sokat várva tehát már egyenes vonalú egyenletes mozgást végez a test. Ha![\[y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\]](/images/math/4/a/9/4a9b8dc11e053c00a27e1355aa2e0c2f.png)
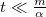, akkor az exponenciálisok argumentumában egy kis szám szerepel. Kihasználva azt a közelítést, miszerint kis 
-re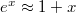 
, megadhatunk egy közelítő formulát a sebességre. Az elmozdulás az ilyen rendű közelítésben csak![\[v\left(t\ll \frac{m}{\alpha}\right)\approx \frac{gm}{\alpha}\left(1-\frac{\alpha}{m}t-1\right)= -gt\]](/images/math/8/9/0/8900e78c445d63dbc1bcf32f91dbca4e.png)
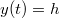lenne. A közelítés következő rendjében 
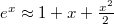, amely szerint Kis időkre tehát úgy viselkedik a test, mintha nem is hatna rá közegellenállás. Ez érthető is, hiszen ebben az idő tartományban még nagyon kicsi a sebesség és így kicsi a vele arányos közegellenállási erő.![\[y\left(t\ll \frac{m}{\alpha}\right)\approx h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1+\frac{\alpha}{m}t-\frac{1}{2}\left(\frac{\alpha}{m}t\right)^{2}\right)=h-\frac{g}{2}t^{2}\,.\]](/images/math/3/6/c/36ce98579e2c15f4ffcac1b1cd527f73.png)
- c) A test teljes energiája szerint változik az időben.
![\[E(t)=mgy(t)+\frac{1}{2}mv(t)^{2}=mg\left[h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\right]+\frac{g^{2}m^{3}}{2\alpha^{2}}\left(e^{-\frac{\alpha}{m}t}-1\right)^{2}\]](/images/math/4/a/3/4a3d907c7206375cd2ed561374de9e53.png)
- a) A testre csak a függőlegesen lefelé irányított gravitációs és a függőlegesen felfelé irányított közegellenállási erők hatnak. A függőleges irányú mozgásegyenlet tehát
