„Erőtan II. - 6.8” változatai közötti eltérés
A Fizipedia wikiből
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
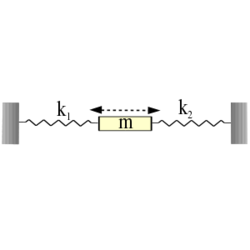
| − | </noinclude><wlatex># | + | </noinclude><wlatex># (6.8) Határozzuk meg a vízszintes síkon mozgó $m$ tömegű test rezgéseinek frekvenciáját, ha az ábrán látható módon két, elhanyagolható tömegű rugóhoz van kapcsolva (rugóállandók: $k_1$ és $k_2$ )! [[Kép:Kfgy1_6_8.svg|none|250px]]</wlatex><includeonly><wlatex>{{Végeredmény|content=$$\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}$$}}</wlatex></includeonly><noinclude> |
| − | </wlatex><includeonly><wlatex>{{Végeredmény|content=$$\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}$$}}</wlatex></includeonly><noinclude> | + | |
== Megoldás == | == Megoldás == | ||
<wlatex>#: A testet egyensúlyi helyzetéből $x$ távolságra kimozdítva ($x$ pozitív, ha jobbra mozdítottuk ki) a mozgásegyenlete $$ma=F_{2}-F_{1}=k_{2}(\Delta l_{02}-x)-k_{1}(\Delta l_{01}+x)$$ alakban írható, ahol $\Delta l_{01}$ és $\Delta l_{02}$ rugók kezdeti megnyúlása, melyekre azonban teljesül $k_{1}\Delta l_{01}=k_{2}\Delta l_{02}$, így a mozgásegyenlet $$m\ddot{x}=-x(k_{1}+k_{2})\,.$$ A rezgések frekvenciája tehát $$\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}\,.$$ | <wlatex>#: A testet egyensúlyi helyzetéből $x$ távolságra kimozdítva ($x$ pozitív, ha jobbra mozdítottuk ki) a mozgásegyenlete $$ma=F_{2}-F_{1}=k_{2}(\Delta l_{02}-x)-k_{1}(\Delta l_{01}+x)$$ alakban írható, ahol $\Delta l_{01}$ és $\Delta l_{02}$ rugók kezdeti megnyúlása, melyekre azonban teljesül $k_{1}\Delta l_{01}=k_{2}\Delta l_{02}$, így a mozgásegyenlet $$m\ddot{x}=-x(k_{1}+k_{2})\,.$$ A rezgések frekvenciája tehát $$\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}\,.$$ | ||
</wlatex> | </wlatex> | ||
</noinclude> | </noinclude> | ||
A lap jelenlegi, 2013. augusztus 27., 21:29-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (6.8) Határozzuk meg a vízszintes síkon mozgó
tömegű test rezgéseinek frekvenciáját, ha az ábrán látható módon két, elhanyagolható tömegű rugóhoz van kapcsolva (rugóállandók: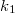 
és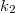 
)! 
Megoldás
- A testet egyensúlyi helyzetéből
távolságra kimozdítva ( pozitív, ha jobbra mozdítottuk ki) a mozgásegyenlete alakban írható, ahol![\[ma=F_{2}-F_{1}=k_{2}(\Delta l_{02}-x)-k_{1}(\Delta l_{01}+x)\]](/images/math/5/4/c/54c26d4782a819b09b5606b5de2a5f4b.png)
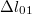és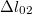 
rugók kezdeti megnyúlása, melyekre azonban teljesül 
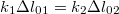, így a mozgásegyenlet A rezgések frekvenciája tehát![\[m\ddot{x}=-x(k_{1}+k_{2})\,.\]](/images/math/a/5/9/a59386a76331defbf1f281f183fd23ba.png)
![\[\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}\,.\]](/images/math/3/2/f/32f80cbc3bd952e0070928541bc59dd0.png)
- A testet egyensúlyi helyzetéből
