„Mechanika - Jegesmedve jégtáblán” változatai közötti eltérés
A Fizipedia wikiből
(→Feladat) |
|||
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
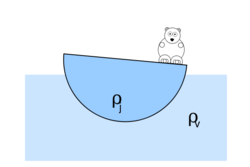
| − | </noinclude><wlatex># (*5.14.) | + | </noinclude><wlatex># (**5.14.) Legalább mekkora (m, V, vagy R) félgömb alakú "jégtábla" képes stabilan megtartani egy 300 kg-os jegesmedvét, ha az a tábla körlapjának közepén áll? Legalább mekkora kell legyen a jégtábla, ha a medve szeretne kisétálni a szélére anélkül, hogy víz érné?Legalább mekkora kell legyen a tapadási súrlódási együttható, hogy még ekkor se csússzon meg a tábla felszínén? ($\rho_{\text{jég}}=0,9\rho_{\text{víz}}$) [[Kép:Kfgy1-5-14.svg|none|250px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=Használjuk ki, hogy a vízbe merülő gömbsüvegrész tömegközéppontja hogyan viselkedik a tábla elfordulásakor.}}{{Végeredmény|content=A megoldást házi feladatként várjuk.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A jégtábla legkisebb lehetséges térfogata $V=10\frac m{\rho_{\text{víz}}}$, ahol $m$ a medve tömege, ha a medve a tábla tömegközéppontja felett áll. Ha a tábla szélén áll, | + | <wlatex>A jégtábla legkisebb lehetséges térfogata $V=10\frac m{\rho_{\text{víz}}}$, ahol $m$ a medve tömege, ha a medve a tábla tömegközéppontja felett áll. Ha a tábla szélén áll, a jégfelszín körlapjának egy pontja éppen érinti a vízfelszínt. A további részletes megoldást házi feladatként várjuk.</wlatex> |
| − | A további részletes megoldást | + | |
</noinclude> | </noinclude> | ||
A lap 2014. november 14., 19:11-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (**5.14.) Legalább mekkora (m, V, vagy R) félgömb alakú "jégtábla" képes stabilan megtartani egy 300 kg-os jegesmedvét, ha az a tábla körlapjának közepén áll? Legalább mekkora kell legyen a jégtábla, ha a medve szeretne kisétálni a szélére anélkül, hogy víz érné?Legalább mekkora kell legyen a tapadási súrlódási együttható, hogy még ekkor se csússzon meg a tábla felszínén? (
) 
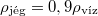Megoldás
A jégtábla legkisebb lehetséges térfogata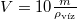 
, ahol 
a medve tömege, ha a medve a tábla tömegközéppontja felett áll. Ha a tábla szélén áll, a jégfelszín körlapjának egy pontja éppen érinti a vízfelszínt. A további részletes megoldást házi feladatként várjuk.
