„Mechanika - Rezgő merev rúd feszültségállapota” változatai közötti eltérés
A Fizipedia wikiből
| 8. sor: | 8. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
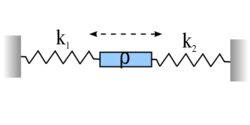
| − | </noinclude><wlatex># (5.15.) | + | </noinclude><wlatex># (5.15.)* Egy $\rho$ sűrűségű, $A$ keresztmetszetű és $l$ hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben. Bizonyítsuk be, hogy a mechnaikai feszültség a rúd mentén lineárisan változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?[[Kép:Kfgy1-5-15.svg|none|250px]]</wlatex><includeonly><wlatex>{{Útmutatás|content=Írjuk fel a Newton-féle mozgásegyenletet a rúd egy kis $dx$ hosszúságú darabjára!}}{{Végeredmény|content=Mivel a test merev, a gyorsulás független a helytől, ezért a mechanikai feszültség csak lineárisan változhat. A rúd végein a feszültség és a keresztmetszet szorzata egyenlő kell legyen az (időfüggő!) rugóerőkkel.}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
<wlatex>megoldás szövege</wlatex> | <wlatex>megoldás szövege</wlatex> | ||
</noinclude> | </noinclude> | ||
A lap 2014. január 7., 13:17-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.15.)* Egy
sűrűségű, 
keresztmetszetű és 
hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben. Bizonyítsuk be, hogy a mechnaikai feszültség a rúd mentén lineárisan változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?
Megoldás
megoldás szövege
