„Deriválás - Egyváltozós vektorfüggvény” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő: Bácsi Ádám {{Kísérleti fizika gyakorlat | tárgynév = Kísérleti fizika…”) |
|||
| 7. sor: | 7. sor: | ||
}} | }} | ||
== Feladat == | == Feladat == | ||
| − | </noinclude><wlatex># | + | </noinclude><wlatex># Tekintsük az alábbi, valós számokról a 3 dimenziós vektorok terébe képező függvényt! |
#: $$ \vec{v}(s) = \left( \begin{array}{c} \sin s \\ 2 \cos s \\ 3 s \end{array} \right) $$ | #: $$ \vec{v}(s) = \left( \begin{array}{c} \sin s \\ 2 \cos s \\ 3 s \end{array} \right) $$ | ||
#: a) Határozzuk meg ennek a $\vec{v}'(s) = \frac{d \vec{v}}{d s}$ deriváltját! | #: a) Határozzuk meg ennek a $\vec{v}'(s) = \frac{d \vec{v}}{d s}$ deriváltját! | ||
A lap jelenlegi, 2014. szeptember 9., 14:24-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Deriválás |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Tekintsük az alábbi, valós számokról a 3 dimenziós vektorok terébe képező függvényt!
-
![\[ \vec{v}(s) = \left( \begin{array}{c} \sin s \\ 2 \cos s \\ 3 s \end{array} \right) \]](/images/math/1/a/3/1a367492fb5e22fda7e649402c2a9c7c.png)
- a) Határozzuk meg ennek a
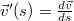 deriváltját!
deriváltját!
- b) Mekkora szöget zárnak be az
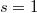 helyen a
helyen a 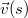 és
és 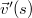 vektorok?
vektorok?
-
Megoldás
- a) Vektorokat komponensenként deriválhatunk, így:
-
![\[ \vec{v}'(s) = \left( \begin{array}{c} \cos s \\ - 2 \sin s \\ 3 \end{array} \right) \]](/images/math/d/2/e/d2edd76d4ae9f940d5b846233e2094bd.png)
- b) A vektorok által bezárt szög koszinusza:
-
![\[ \cos(\varphi) = \frac{\vec{v}(s) \cdot \vec{v}'(s)}{| \vec{v}(s)| \, |\vec{v}'(s)|}\]](/images/math/0/8/d/08de8589664517a1b7f202f9cb10678d.png)
- Behelyettesítve az
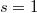 értéket:
értéket:
-
![\[ \vec{v}(s) = \left( \begin{array}{c} 0.841 \\ 1.081 \\ 3.0 \end{array} \right) \; , \quad \vec{v}'(s) = \left( \begin{array}{c} 0.540 \\ -1.683 \\ 3.0 \end{array} \right) \]](/images/math/5/4/5/545d9378ccf701594f82e22d316ee77e.png)
-
![\[ \cos(\varphi) = \frac{0.841 \cdot 0.540 - 1.081 \cdot 1.683 + 3.0 \cdot 3.0}{\sqrt{0.841^2 + 1.081^2 + 3.0^2} \, \sqrt{0.540^2 + 1.683^2 + 3.0^2}} = 0.665 \]](/images/math/3/d/d/3ddc2adc2a0d61bc25999fbc28fb8dbc.png)
- Ebből