„Mechanika - Jegesmedve jégtáblán” változatai közötti eltérés

A lap 2014. november 14., 19:11-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) ← Régebbi szerkesztés		A lap 2015. október 28., 15:11-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) Újabb szerkesztés →
11. sor:		11. sor:
	== Megoldás ==		== Megoldás ==
−	<wlatex>A jégtábla legkisebb lehetséges térfogata $V=10\frac m{\rho_{\text{víz}}}$, ahol $m$ a medve tömege, ha a medve a tábla tömegközéppontja felett áll. Ha a tábla szélén áll, a jégfelszín körlapjának egy pontja éppen érinti a vízfelszínt. A további részletes megoldást házi feladatként várjuk.</wlatex>	+	<wlatex>A jégtábla legkisebb lehetséges térfogata $V=10\frac m{\rho_{\text{víz}}}$, ahol $m$ a medve tömege, ha a medve a tábla tömegközéppontja felett áll. A jégtábla sugara $R=1,127\,\rm m$, tömege pedig $m_{\text{jég}}= 2700\,\rm{kg}$. Ha a tábla szélén áll, a jégfelszín körlapjának egy pontja éppen érinti a vízfelszínt, és a körlap vízszintessel bezárt szögét jelöljük $\alpha$-val. [[Kép:Kfgy1-5-14m.svg|none|350px]] A rajz alapján a bemerülő rész mélysége $h=R(1-\sin\alpha)$, a medve és a felhajtóerő hatásvonalának távolsága $r=R\cos\alpha$. A jégtábla nehézségi ereje a félgömb tömegközéppontjában támad, ennek távolsága a görbületi középpontól (mely a teljes gömb közepe lenne) integrálással határozható meg: $z=\frac 38 R$, így az erő hatásvonalának távolsága a feljhatóerőétől $d=\frac 38 R\sin\alpha$. Szükség van még a bemerülő rész térfogatára, amely a matekkönyvek szerint $$V_{\rm{be}}=(3r^2+h^2)\frac{h\pi}{6},$$ illetve félgömb teljes térfogatára. Az eddigieket felhasználva most már fel lehet írni az erők egyensúlyát: $$\rho_{\rm{v}}V_{\rm{be}}g=mg+\rho_{\rm{v}}0,9\left(\frac 23R^3\pi\right)g,$$ valamint a görbületi középpontra vonatkoztatva a forgatónyomatétok egyensúlyát: $$mgR\cos\alpha=0,9\rho_{\rm{v}}\left(\frac 23R^3\pi\right)gR\frac 38\sin\alpha.$$ Ez a két egyenlet elvileg megoldható az $R$ és $\alpha$ ismeretlenekre, azonban a megoldás nem végezhető el teljesen elemi úton. A nyomatéki egyenletből kifejezhető a medve tömege a többi paraméterrel, és behelyettesíthető az erőegyenletbe, így az $R$ változó kiejthető. A megmaradt egyenlet $\alpha$-ra csak numerikusan oldható meg, ennek eredménye $\alpha=3,12^{\rm o }$ vagy $0,0545$ radián. Mivel ez a szög kicsi, egyben a tangensének is vehető, ennél kell nagyobb vagy egyenlőnek lennie a súrlódási együtthatónak. A megoldás további eredményei: $R=1,981\,\rm m$, $V_{\text{jég}}=16,28\,\rm{m^3}$, $V_{\rm{be}}=14,938\,\rm{m^3}$, valamint $m_{\text{jég}}=14652\,\rm{kg}$, amely $5,43$-szorosa a korábbi esetének, amikor a medve középen marad.</wlatex>
	</noinclude>		</noinclude>

---

A lap 2015. október 28., 15:11-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Rugalmasság, folyadékok
Feladatok listája: Tengerbe lógatott drótkötél Fémhuzal önsúllyal Rugalmas energia sűrűsége Rezgő merev rúd feszültségállapota Rétegezett folyadékok Vízbe merített farúd Medencefal terhelése Fagolyó vízcsőben Forgó folyadék felszíne Folyadékóra Kifolyás sebessége Lamináris áramlás Jegesmedve jégtáblán
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

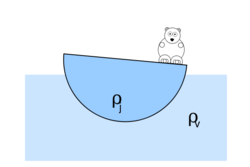
Feladat

1. (**5.14.) Legalább mekkora (m, V, vagy R) félgömb alakú "jégtábla" képes stabilan megtartani egy 300 kg-os jegesmedvét, ha az a tábla körlapjának közepén áll? Legalább mekkora kell legyen a jégtábla, ha a medve szeretne kisétálni a szélére anélkül, hogy víz érné?Legalább mekkora kell legyen a tapadási súrlódási együttható, hogy még ekkor se csússzon meg a tábla felszínén? ()
   

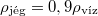Megoldás

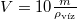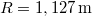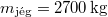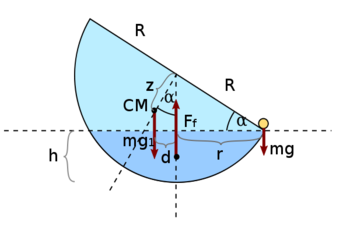
A jégtábla legkisebb lehetséges térfogata , ahol a medve tömege, ha a medve a tábla tömegközéppontja felett áll. A jégtábla sugara , tömege pedig . Ha a tábla szélén áll, a jégfelszín körlapjának egy pontja éppen érinti a vízfelszínt, és a körlap vízszintessel bezárt szögét jelöljük -val. A rajz alapján a bemerülő rész mélysége 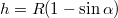, a medve és a felhajtóerő hatásvonalának távolsága 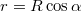. A jégtábla nehézségi ereje a félgömb tömegközéppontjában támad, ennek távolsága a görbületi középpontól (mely a teljes gömb közepe lenne) integrálással határozható meg: 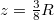, így az erő hatásvonalának távolsága a feljhatóerőétől 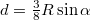. Szükség van még a bemerülő rész térfogatára, amely a matekkönyvek szerint illetve félgömb teljes térfogatára. Az eddigieket felhasználva most már fel lehet írni az erők egyensúlyát: valamint a görbületi középpontra vonatkoztatva a forgatónyomatétok egyensúlyát: Ez a két egyenlet elvileg megoldható az és ismeretlenekre, azonban a megoldás nem végezhető el teljesen elemi úton. A nyomatéki egyenletből kifejezhető a medve tömege a többi paraméterrel, és behelyettesíthető az erőegyenletbe, így az változó kiejthető. 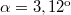A megmaradt egyenlet -ra csak numerikusan oldható meg, ennek eredménye vagy 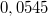radián. Mivel ez a szög kicsi, egyben a tangensének is vehető, ennél kell nagyobb vagy egyenlőnek lennie a súrlódási együtthatónak. A megoldás további eredményei: 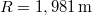, , 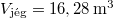, 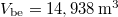valamint 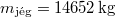, amely 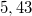-szorosa a korábbi esetének, amikor a medve középen marad.