„Mechanika - Forgó folyadék felszíne” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév = …”) |
|||
| 10. sor: | 10. sor: | ||
</noinclude><wlatex># (5.9.) Egy $R$ sugarú, függőleges helyzetű henger a benne lévő folyadékkal együtt függőleges tengely körül $\omega$ szögsebességgel forog. Milyen alakot vesz fel a folyadék felszíne?</wlatex><includeonly><wlatex>{{Útmutatás|content=Vizsgáljuk a folyadékot forgó vonatkoztatási rendszerben. Az eredő gravitációs és tehetetlenségi tér sugárfüggő a forgástengelytől mérve.}}{{Végeredmény|content=Forgási paraboloid.}}</wlatex></includeonly><noinclude> | </noinclude><wlatex># (5.9.) Egy $R$ sugarú, függőleges helyzetű henger a benne lévő folyadékkal együtt függőleges tengely körül $\omega$ szögsebességgel forog. Milyen alakot vesz fel a folyadék felszíne?</wlatex><includeonly><wlatex>{{Útmutatás|content=Vizsgáljuk a folyadékot forgó vonatkoztatási rendszerben. Az eredő gravitációs és tehetetlenségi tér sugárfüggő a forgástengelytől mérve.}}{{Végeredmény|content=Forgási paraboloid.}}</wlatex></includeonly><noinclude> | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A tengelytől $x$ távolságban a forgó rendszerben egy $\omega^2x$ nagyságú vízszintes tehetetlenségi gyorsulást észlelünk. Ezt a nehézkedéshez hozzávéve bevezethetünk egy eredő nehézkedési+tehetetlenségi teret. Legyen az y-tengely függőleges, az x-tengely pedig vízszintes: $$\vec g*=-g\vec e_y+\omega^2x\vec e_x$$ Erre lesz merőleges a folyadékfelszín minden pontban, tehát a felszín vízszintessel bezárt szögére $$\tan{\alpha}=\frac{\text{d}y}{\text{d}x}=\frac{\omega^2x}g,$$ melyből $$y(x)=\frac{\omega^2x^2}{2g}+y_0,$$ ha $(x | + | <wlatex>A tengelytől $x$ távolságban a forgó rendszerben egy $\omega^2x$ nagyságú vízszintes tehetetlenségi gyorsulást észlelünk. Ezt a nehézkedéshez hozzávéve bevezethetünk egy eredő nehézkedési+tehetetlenségi teret. Legyen az y-tengely függőleges, az x-tengely pedig vízszintes: $$\vec g*=-g\vec e_y+\omega^2x\vec e_x$$ Erre lesz merőleges a folyadékfelszín minden pontban, tehát a felszín vízszintessel bezárt szögére $$\tan{\alpha}=\frac{\text{d}y}{\text{d}x}=\frac{\omega^2x}g,$$ melyből $$y(x)=\frac{\omega^2x^2}{2g}+y_0,$$ ha $(x\leq R)$. Azaz a vízfelszín alakja egy forgási paraboloid.</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2012. november 15., 16:53-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.9.) Egy
sugarú, függőleges helyzetű henger a benne lévő folyadékkal együtt függőleges tengely körül 
szögsebességgel forog. Milyen alakot vesz fel a folyadék felszíne?
Megoldás
A tengelytől
távolságban a forgó rendszerben egy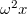 
nagyságú vízszintes tehetetlenségi gyorsulást észlelünk. Ezt a nehézkedéshez hozzávéve bevezethetünk egy eredő nehézkedési+tehetetlenségi teret. Legyen az y-tengely függőleges, az x-tengely pedig vízszintes: ![\[\vec g*=-g\vec e_y+\omega^2x\vec e_x\]](/images/math/c/5/5/c55227fb9ae4d367ce35dcb69685733f.png)
![\[\tan{\alpha}=\frac{\text{d}y}{\text{d}x}=\frac{\omega^2x}g,\]](/images/math/4/6/2/4624d61d4b1b577984daee62dcd11cc1.png)
![\[y(x)=\frac{\omega^2x^2}{2g}+y_0,\]](/images/math/1/0/4/10407d2075d23b0c4f155986b9a2c800.png)
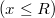. Azaz a vízfelszín alakja egy forgási paraboloid.
