„Erőtan II. - 4.2” változatai közötti eltérés

A lap 2013. április 12., 23:21-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Erőtan II.
Feladatok listája: Erőtan II. - 2.1.21 Erőtan II. - 2.1.23 Erőtan II. - 4.2 Erőtan II. - 4.3 Erőtan II. - 4.4 Erőtan II. - 4.8 Erőtan II. - 4.13 Erőtan II. - 4.24 Erőtan II. - 4.37 Erőtan II. - 6.7 Erőtan II. - 6.8 Erőtan II. - 6.10 Erőtan II. - Forgó rotor még egyszer Erőtan II. - Coriolis
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Egy egyenletes sebességgel mozgó kocsin egyensúlyi helyzetben áll egy 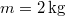$\setbox0\hbox{$m=2\,\mathrm{kg}$}% \message{//depth:\the\dp0//}% \box0%$ tömegű matematikai inga. A fonál szakító szilárdsága 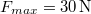$\setbox0\hbox{$F_{max}=30\,\mathrm{N}$}% \message{//depth:\the\dp0//}% \box0%$ . A kocsit hirtelen gyorsítani kezdjük. Mi történik az ingával? Mekkora (időben állandó) gyorsulást adhatunk a kocsinak, hogy a fonál még éppen ne szakadjon el?

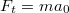A gyorsítás hatására a kocsihoz rögzített vonatkoztatási rendszerben egy vízszintes irányú, $\setbox0\hbox{$F_{t}=ma_{0}$}% \message{//depth:\the\dp0//}% \box0%$ nagyságú tehetetlenségi erő is hat az ingára. Így a kezdeti időpillanatban az eredő erő nem zérus, az inga nincs egyensúlyban, tehát elkezd lengeni. A lengés során akkor a legnagyobb a kötelet feszítő erő, amikor a kocsihoz rögzített vonatkoztatási rendszerben a rá ható erők eredője zérus. Ezt a szituációt ábrázoltuk az ÁBRÁn.

ÁBRA

$K^{2}=F_{t}^{2}+F_{g}^{2}$

A kötél véges szakító szilárdsága miatt

$K\leq F_{max}\qquad\Rightarrow\qquad a_{0}\leq\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}\,,$

vagyis a maximális gyorsítás

$a_{0max}=\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}$

lehet.

@@ 13. sor: / 13. sor: @@
 <wlatex>#: A gyorsítás hatására a kocsihoz rögzített vonatkoztatási rendszerben egy vízszintes irányú, $F_{t}=ma_{0}$ nagyságú tehetetlenségi erő is hat az ingára. Így a kezdeti időpillanatban az eredő erő nem zérus, az inga nincs egyensúlyban, tehát elkezd lengeni. A lengés során akkor a legnagyobb a kötelet feszítő erő, amikor a kocsihoz rögzített vonatkoztatási rendszerben a rá ható erők eredője zérus. Ezt a szituációt ábrázoltuk az ÁBRÁn.
 ÁBRA
-$$K^{2}=F_{t}^{2}+F_{g}^{2}$$ A kötél véges szakító szilárdsága miatt $$K\leq F_{max}\qquad\Rightarrow\qquad a_{0}\leq\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}\,,$$ vagyis a maximális gyorsítás $$a_{0max}=\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}$$ lehet.{2g}$$
+$$K^{2}=F_{t}^{2}+F_{g}^{2}$$ A kötél véges szakító szilárdsága miatt $$K\leq F_{max}\qquad\Rightarrow\qquad a_{0}\leq\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}\,,$$ vagyis a maximális gyorsítás $$a_{0max}=\sqrt{\left(\frac{F_{\max}}{m}\right)^{2}-g^{2}}$$ lehet.
 </wlatex>
 </noinclude>