„Mechanika - Rugalmasság, folyadékok” változatai közötti eltérés
A Fizipedia wikiből
| 17. sor: | 17. sor: | ||
{{:Mechanika - Fagolyó vízcsőben}}{{Megoldás|link=Mechanika - Fagolyó vízcsőben}} | {{:Mechanika - Fagolyó vízcsőben}}{{Megoldás|link=Mechanika - Fagolyó vízcsőben}} | ||
{{:Mechanika - Forgó folyadék felszíne}}{{Megoldás|link=Mechanika - Forgó folyadék felszíne}} | {{:Mechanika - Forgó folyadék felszíne}}{{Megoldás|link=Mechanika - Forgó folyadék felszíne}} | ||
| − | |||
{{:Mechanika - Folyadékóra}}{{Megoldás|link=Mechanika - Folyadékóra}} | {{:Mechanika - Folyadékóra}}{{Megoldás|link=Mechanika - Folyadékóra}} | ||
{{:Mechanika - Kifolyás sebessége}}{{Megoldás|link=Mechanika - Kifolyás sebessége}} | {{:Mechanika - Kifolyás sebessége}}{{Megoldás|link=Mechanika - Kifolyás sebessége}} | ||
{{:Mechanika - Lamináris áramlás}}{{Megoldás|link=Mechanika - Lamináris áramlás}} | {{:Mechanika - Lamináris áramlás}}{{Megoldás|link=Mechanika - Lamináris áramlás}} | ||
{{:Mechanika - Jegesmedve jégtáblán}}{{Megoldás|link=Mechanika - Jegesmedve jégtáblán}} | {{:Mechanika - Jegesmedve jégtáblán}}{{Megoldás|link=Mechanika - Jegesmedve jégtáblán}} | ||
A lap 2014. január 7., 14:36-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
Gyakorlatok listája:
|
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (5.1.) Egy hajóról a
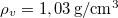 sűrűségű tengerbe lógatnak függőlegesen egy
sűrűségű tengerbe lógatnak függőlegesen egy 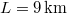 hosszú drótkötelet (keresztmetszete
hosszú drótkötelet (keresztmetszete 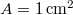 , sűrűsége
, sűrűsége 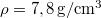 , szakítószilárdsága
, szakítószilárdsága 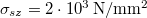 ). Elszakad-e a kötél?
). Elszakad-e a kötél?
- (*5.2.) Egy erőmentes állapotban
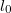 hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége
hosszúságú, vékony fémhuzalt egyik végénél fogva függőleges helyzetben lelógatunk. A fém sűrűsége  , Young-modulusa
, Young-modulusa  , egyenletes keresztmetszete pedig
, egyenletes keresztmetszete pedig  .
.
- a) Mennyivel változik meg a huzal hossza?
- b) Mennyi lesz a megnyúlás, ha a huzal alsó végére egy m tömegű testet akasztunk?
- (5.3.) Egy eredetileg
 hosszúságú,
hosszúságú,  keresztmetszetű,
keresztmetszetű,  Young-modulusú huzalt a rugalmassági határon belül
Young-modulusú huzalt a rugalmassági határon belül  ? rugalmas feszültséggel terhelünk. Mennyi a huzalban tárolt rugalmas energia térfogati sűrűsége?
? rugalmas feszültséggel terhelünk. Mennyi a huzalban tárolt rugalmas energia térfogati sűrűsége?
- (*5.15.) Egy
 sűrűségű,
sűrűségű,  keresztmetszetű és
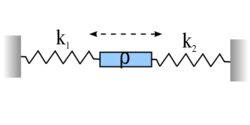
keresztmetszetű és  hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben, és egyensúlyi helyzetében mindkét rugó nyújtatlan. Bizonyítsuk be, hogy a mechanikai feszültség a rúd mentén egyenletesen változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?
hosszúságú homogén merev rudat az ábra szerint két rugó közé teszünk. A rúd a rugók egyenesében rezeghet, például egy súrlódásmentes csőben, és egyensúlyi helyzetében mindkét rugó nyújtatlan. Bizonyítsuk be, hogy a mechanikai feszültség a rúd mentén egyenletesen változik és tetszőleges helyen nézve rezgést végez. Hol van mindenkor feszültségmentes keresztmetszet, és hol vannak szélsőértékek a feszültségben?
- (5.5.) Egy edényben lévő
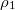 sűrűségű folyadék fölé
sűrűségű folyadék fölé 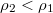 sűrűségű folyadékot rétegeznek. A két folyadék határán egy
sűrűségű folyadékot rétegeznek. A két folyadék határán egy  térfogatú,
térfogatú,  sűrűségű test lebeg. A test térfogatának mekkora része merül a nagyobb sűrűségű folyadékba?
sűrűségű test lebeg. A test térfogatának mekkora része merül a nagyobb sűrűségű folyadékba?
- (5.6.) Vékony, egyenletes
 keresztmetszetű,
keresztmetszetű,  hosszúságú fa rudat egyik végénél minden irányban elforgatható módon felfüggesztünk, másik végét pedig vízbe merítjük az ábra szerint. Mennyi a rúd vízből kiálló részének
hosszúságú fa rudat egyik végénél minden irányban elforgatható módon felfüggesztünk, másik végét pedig vízbe merítjük az ábra szerint. Mennyi a rúd vízből kiálló részének  hossza, ha a rúd sűrűsége
hossza, ha a rúd sűrűsége 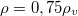 ?
?
- (*5.7.) Mekkora vízszintes irányú erőt fejt ki a
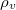 sűrűségű folyadék egy medence függőleges, sík falára, ha a vízmagasság
sűrűségű folyadék egy medence függőleges, sík falára, ha a vízmagasság  , a fal hosszúsága pedig
, a fal hosszúsága pedig  ? Milyen magasságban van az eredő erő támadáspontja?
? Milyen magasságban van az eredő erő támadáspontja?
- (5.8.) Egy vízzel töltött, mindkét végén lezárt vízszintes üvegcsőben egy fagolyó van. A golyó térfogata
 , sűrűsége pedig
, sűrűsége pedig  . Az üvegcső vízszintes irányban egyenletes sebességgel mozog.
. Az üvegcső vízszintes irányban egyenletes sebességgel mozog.
- a) Merre mozdul el a golyó, ha az üvegcsövet lefékezzük?
- b) Mekkora a golyóra a gyorsulás kezdetén ható vízszintes erő, ha a gyorsulás nagysága
 ?
?
- (5.9.) Egy
 sugarú, függőleges helyzetű henger a benne lévő folyadékkal együtt függőleges tengely körül
sugarú, függőleges helyzetű henger a benne lévő folyadékkal együtt függőleges tengely körül  szögsebességgel forog. Milyen alakot vesz fel a folyadék felszíne? (A kanadai Large Zenith Telescope higannyal töltött kör alakú medencéje 8,5 fordulat/perc sebességgel forog. Mekkora az így képzett tükör fókusztávolsága?)
szögsebességgel forog. Milyen alakot vesz fel a folyadék felszíne? (A kanadai Large Zenith Telescope higannyal töltött kör alakú medencéje 8,5 fordulat/perc sebességgel forog. Mekkora az így képzett tükör fókusztávolsága?)
- (5.11.) A homokóra mintájára "folyadékórát" készítünk. A folyadékóra tartályának alján kicsi,
 keresztmetszetű lyukon folyik ki a folyadék. Milyen alakú forgástestté kell kiképezni az edényt, ha azt akarjuk, hogy a folyadék felszíne állandó
keresztmetszetű lyukon folyik ki a folyadék. Milyen alakú forgástestté kell kiképezni az edényt, ha azt akarjuk, hogy a folyadék felszíne állandó 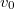 sebességgel süllyedjen?
sebességgel süllyedjen?
- (5.12.) Egy magas, nagy
 keresztmetszetű, vízzel teli edény oldalán, az aljához közel, kis
keresztmetszetű, vízzel teli edény oldalán, az aljához közel, kis 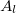 felületű lyukon folyik ki a víz. Az edény keresztmetszete sokkal nagyobb a lyukénál, a víz magassága a lyuk fölött
felületű lyukon folyik ki a víz. Az edény keresztmetszete sokkal nagyobb a lyukénál, a víz magassága a lyuk fölött  . Milyen sebességgel hagyja el a víz a lyukat, ha a folyadék súrlódásmentesen mozog?
. Milyen sebességgel hagyja el a víz a lyukat, ha a folyadék súrlódásmentesen mozog?
- (5.13.) Vízszintes helyzetű, párhuzamos síklemezek között
 vastagságú folyadékréteg van. A felső lemezt
vastagságú folyadékréteg van. A felső lemezt 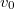 állandó sebességgel mozgatjuk, az alsó lemez nyugalomban van. Mekkora a mozgó lemeztől
állandó sebességgel mozgatjuk, az alsó lemez nyugalomban van. Mekkora a mozgó lemeztől  távolságban a folyadék sebessége?
távolságban a folyadék sebessége?
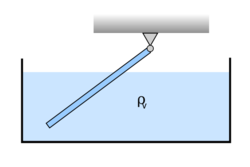
- (**5.14.) Legalább mekkora (m, V, vagy R) félgömb alakú "jégtábla" képes stabilan megtartani egy 300 kg-os jegesmedvét, ha az a tábla körlapjának közepén áll? Legalább mekkora kell legyen a jégtábla, ha a medve szeretne kisétálni a szélére anélkül, hogy víz érné?Legalább mekkora kell legyen a tapadási súrlódási együttható, hogy még ekkor se csússzon meg a tábla felszínén? (
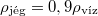 )
)
![\[\Delta l=\frac{\rho l_0^2g}{2E}\]](/images/math/d/f/b/dfb5542cdb2e112f42e8d3ff3e83af6b.png)
![\[\Delta l_2=\Delta l+\frac{mg}{EA}l_0\]](/images/math/3/7/e/37e7e530bb9d799f575d73019534bd66.png)
![\[w_r=\frac{\sigma^2}{2E}\]](/images/math/a/6/3/a6395c9caa48cb1694e7fbd9a9bad949.png)
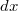 hosszúságú darabjára!
hosszúságú darabjára! ![\[V_1=\frac{\rho-\rho_2}{\rho_1-\rho_2}V\]](/images/math/b/f/c/bfc2c6407da74462e2d00e2a30c28456.png)
![\[x=\frac L2\]](/images/math/c/1/f/c1f6139f4dd53acc2854dab1ae387200.png)
![\[F_e=\rho_vgL\frac{h^2}2\]](/images/math/2/4/a/24a5fb4a01fb48142c6dee53788f6175.png)
![\[\frac h3\]](/images/math/a/e/7/ae7998c299ed89dbc56c73232660d025.png)
![\[F=(\rho_v-\rho)Va\]](/images/math/3/9/9/399f24940c14fde11058f03b206e01ac.png)
![\[h(r)=\frac{v_0^2}{2g}\left(\frac{\pi^2r^4}{A^2}-1\right)\]](/images/math/4/f/f/4ff9fbce26228db79c8e2adcfe104bbe.png)
![\[v\approx\sqrt{2gh}\]](/images/math/e/1/9/e199938f626b3b59cabd0ee1b66d1790.png)
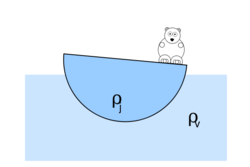
![\[v(x)=v_0\left(1-\frac xd\right)\]](/images/math/4/3/d/43d155e4cf68b11100bff2cc4aa1fb52.png)
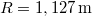 ,
, 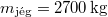 , a második esetben
, a második esetben 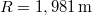 ,
, 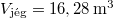 ,
, 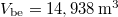 , valamint
, valamint