„Mechanika - Erőtan II.” változatai közötti eltérés
A Fizipedia wikiből
| 21. sor: | 21. sor: | ||
{{:Erőtan II. - 6.10}}{{Megoldás|link=Erőtan II. - 6.10}} | {{:Erőtan II. - 6.10}}{{Megoldás|link=Erőtan II. - 6.10}} | ||
{{:Erőtan II. - Forgó rotor még egyszer}}{{Megoldás|link=Erőtan II. - Forgó rotor még egyszer}} | {{:Erőtan II. - Forgó rotor még egyszer}}{{Megoldás|link=Erőtan II. - Forgó rotor még egyszer}} | ||
| + | {{:Erőtan II. - Coriolis}}{{Megoldás|link=Erőtan II. - Coriolis}} | ||
A lap jelenlegi, 2014. október 8., 11:51-kori változata
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Erőtan II. |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladatok
- (**2.1.21) Egy testre a nehézségi erőn kívül a sebességgel arányos fékező erő hat. (
)
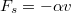- a) Írjuk le a test mozgását, ha
magasságból kezdősebesség nélkül indult!
- b) Milyen lesz a test mozgása
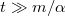és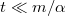 
esetén?
- c) Hogyan változik időben a test teljes energiája? Végeredmény [mutat]
- a) Írjuk le a test mozgását, ha
- (**2.1.23) Milyen magasra emelkedik egy
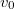sebességgel függőlegesen felhajított test, ha a sebességgel arányos fékező erő (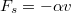) hat rá? Mennyi idő alatt éri el a pálya legmagasabb pontját? Végeredmény [mutat]
- (*4.2) Egy egyenletes sebességgel mozgó kocsin egyensúlyi helyzetben áll egy
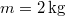tömegű matematikai inga. A fonál szakító szilárdsága 
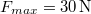. A kocsit hirtelen gyorsítani kezdjük. Mi történik az ingával? Mekkora (időben állandó) gyorsulást adhatunk a kocsinak, hogy a fonál még éppen ne szakadjon el?Végeredmény [mutat]
- (*4.3) Egy vasúti kocsiban
hosszúságú fonálra pontszerű 
tömeget felfüggesztve ingát készítenek. A vasúti kocsi 
időpontban vízszintes pályán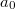 
gyorsulással kezd mozogni. 
, 
, 
.
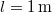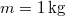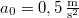- a) Milyennek észleli az tömegű test mozgását a vasúti kocsiban levő megfigyelő?
- b) Külön ábrán jelölje be az tömegű testre - a gyorsuló kocsi koordinátarendszerében - ható erőket, és írja fel a test mozgásegyenletét!
- c) Határozza meg a test mozgását leíró
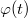függvényt! (A 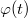függvény jellemző mennyiségeit számszerűen adja meg!)Végeredmény [mutat]
- a) Milyennek észleli az
- (*4.4) Egy hosszúságú, tömegű matematikai ingát mérlegre állítunk. Ha az inga legnagyobb kitérésekor a függőlegessel bezárt szöge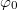
, számítsuk ki, mekkora az inga súlya abban a pillanatban, amikor a függőlegessel bezárt szöge 
.Végeredmény [mutat]
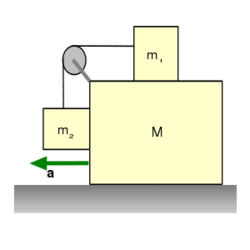
- (4.8) Mekkora gyorsulással kell az
tömeget mozgatni, hogy hozzá képest az 
és 
tömegű testek nyugalomban legyenek? A kötél nyújthatatlan és elhanyagolható tömegű, súrlódás sehol nincs. (4.8. ábra) 
Végeredmény [mutat]
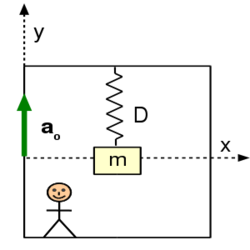
- (*4.13) Egy liftben
direkciós erejű rugóra erősítve egy tömegű testet függesztünk fel. A test a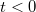 
időpontokban nyugalomban van. A lift a időpontban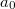 
gyorsulással emelkedni kezd. (4.13. ábra) 
, 
, 
.
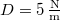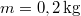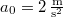- a) Milyennek észleli a test mozgását a liftbeli megfigyelő?
- b) Külön ábrán jelölje be az m tömegű testre - a gyorsuló lift koordinátarendszerében - ható erőket, és írja fel a test mozgásegyenletét az ábrán bejelölt (lifthez rögzített) koordinátarendszerben!
- c) Határozza meg a test mozgását jellemző
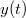függvényt, ha a test az ábra szerinti 
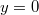koordinátájú pontban történő elhelyezkedése a 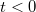időpontokban fennálló egyensúlyi állapotra érvényes! (Az 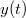függvény jellemző mennyiségeit számszerűen adja meg!)
Végeredmény [mutat]
- (*4.24) Az Egyenlítőn fekvő repülőtéren három teljesen egyforma ingaóra van. Az
ingaóra a repülőtéren marad, a 
ingaórát egy kelet, a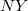 
-t egy nyugat felé induló repülőgépre helyezik. Pontosan délben - amikor mindhárom óra ugyanazt az időt mutatja - a repülőgépek elindulnak és egyenletes sebességgel körberepülik a Földet, úgy, hogy egyszerre érjenek vissza a kiindulási repülőtérre. Visszaérkezésükkor az óra éppen következő nap déli 12 óra 0 perc 0 másodpercet mutat.
- a) Mindhárom óra ugyanezt az időt mutatja-e? Ha nem, soroljunk fel különböző okokat, melyek az időkülönbséget előidézhetik!
- b) A legjelentősebb hatás figyelembevételével adjuk meg, hogy mennyivel fog többet, illetve kevesebbet mutatni a , illetve az 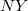óra a 24 órás repülés után!Végeredmény [mutat]
- (*4.37) Egy gázban a molekulák sebességeloszlásának meghatározására a következő mérést végezhetjük (Stern kísérlet). Egy izzítható fémszálat körülveszünk két koaxiális hengerrel, amelyek sugarai
és 
. A belsőn az egyik alkotóján egy keskeny rést hozunk létre. Ha az egész rendszer nyugalomban van, az elpárolgó fém molekulái a réssel szemben a külső henger falán egy egyenes vonal mentén csapódnak le. Ha az egész rendszert 
szögsebességgel forgatjuk, a becsapódó molekulák sebességüktől függő mértékben jobban vagy kevésbé eltérnek ettől a vonaltól. Számítsuk ki az eltérés ívhosszát a részecskék sebességének függvényében!Végeredmény [mutat]
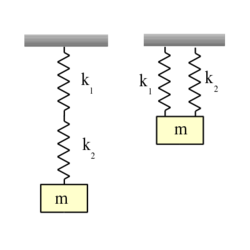
- (6.7.) Határozzuk meg a nehézségi erőtérben az ábrán látható módon a
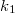és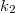 
direkciós erejű rugókra erősített tömegű test rezgési frekvenciáit! 
Végeredmény [mutat]
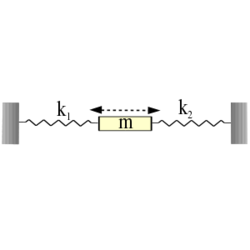
- (6.8) Határozzuk meg a vízszintes síkon mozgó tömegű test rezgéseinek frekvenciáját, ha az ábrán látható módon két, elhanyagolható tömegű rugóhoz van kapcsolva (rugóállandók: 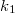és )!
Végeredmény [mutat]
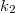- (6.10.) Síklemez a rajta nyugvó testtel együtt harmonikus rezgést végez a vízszintes síkban. A rezgés amplitúdója
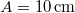. Mekkora a lemez és a test közötti súrlódási együttható, ha a test akkor kezd csúszni a lemezen, amikor a rezgésidő kisebb lesz, mint 
? Végeredmény [mutat]
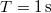- Oldjuk meg az Erőtan I. - 2.4.4 feladatot újból, de most a rotorral együttforgó koordinátarendszerben! Ha
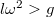, adjuk meg az inga rezgéseinek frekvenciáját, ha kicsit kitérítjük egyensúlyi helyzetéből. (Tegyük fel, hogy az ingát a rotorhoz egy merev rúd köti, ami a rotorral együtt forog.)
- Egy hosszúságú fonal végén tömegű kicsiny test található. A fonal másik végét fogva, szögsebességgel forgatjuk a testet egy vízszintes, súrlódásmentes asztalon. Mekkora a kötélerő? Oldjuk meg a feladatot álló rendszerből nézve, ill az együttforgó rendszerből nézve is. Ezután oldjuk meg a feladatot valamely más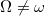
szögsebességgel forgó rendszerből is! Milyen tehetetlenségi erők lépnek fel az egyes esetekben?Végeredmény [mutat]
![\[y(t)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\]](/images/math/0/1/2/0129bae7deed8ea060fbe0a1bb338dd3.png)
![\[y\left(t\gg \frac{m}{\alpha}\right)=h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\]](/images/math/4/a/9/4a9b8dc11e053c00a27e1355aa2e0c2f.png)
![\[y\left(t\ll \frac{m}{\alpha}\right)=h-\frac{g}{2}t^{2}\]](/images/math/a/e/5/ae5cc7eebc6faea049dc858aca846dd4.png)
![\[E(t)=mg\left[h-\frac{gm}{\alpha}t+\frac{gm^{2}}{\alpha^{2}}\left(1-e^{-\frac{\alpha}{m}t}\right)\right]+\frac{g^{2}m^{3}}{2\alpha^{2}}\left(e^{-\frac{\alpha}{m}t}-1\right)^{2}\]](/images/math/5/a/d/5ada9f58bdbb13fc951fdf05261b3b68.png)
![\[y(T)=\frac{mv_{0}}{\alpha}-g\left(\frac{m}{\alpha}\right)^{2}\ln\left(1+\frac{\alpha v_{0}}{gm}\right)\,.\]](/images/math/3/5/2/35231011447a784700938ddcaa2b2263.png)
![\[a_{0max}=6,08\,\rm{m/s^2}\]](/images/math/3/8/1/3815dccb0993e008fee4c205b633e613.png)
![\[\ddot{\varphi}+\omega^{2}\sin(\varphi-\varphi_{0})=0\qquad\qquad \omega^{2}=\frac{\sqrt{g^{2}+a_{0}^{2}}}{l}\]](/images/math/b/8/f/b8f1bae2e60896ac4d19593ca66f4216.png)
![\[\varphi(t)=\varphi_{0}\left(1-\cos(\omega t)\right)\]](/images/math/1/0/8/108811eb473782b43de24a413c206279.png)
![\[G=mg\cos\varphi\big(3\cos\varphi-2\cos\varphi_{0}\big)\]](/images/math/1/c/c/1cc133ea8e09f7228acf905e9d0d22d9.png)
![\[a=\frac{m_{2}}{m_{1}}g\]](/images/math/8/3/d/83d5641fc21ae927e6c09acb2fdb16be.png)
![\[m\ddot{y}=-Dy-ma_{0}\]](/images/math/2/f/1/2f1380d5317cd28cf8943791a2fde176.png)
![\[y(t)=y_{0}(1-\cos(\omega t))\qquad\qquad y_{0}=-0,08\,\mathrm{m}\]](/images/math/6/b/b/6bbf28233898a80cf23a8b0066ef1381.png)
![\[t_{K}=1 \,\mathrm{nap} - 7,33 \,\mathrm{perc}\qquad\qquad t_{NY}=1 \,\mathrm{nap} + 4,87 \,\mathrm{perc}\]](/images/math/8/3/4/8341813ec89b1a5df9afe735443afed1.png)
![\[i=R\omega\frac{R-r}{v}\,.\]](/images/math/8/2/1/821ca6650794163feabb3def510e5b35.png)
![\[\omega=2\pi f=\sqrt{\frac{k_{\rm{eff}}}m},\]](/images/math/b/3/a/b3a00729c5df2d82c0b667932dd9aadb.png)
![\[k_{\rm{eff}}=k_1+k_2,\]](/images/math/4/5/7/4573653343b4a62118c0aa51078a26d9.png)
![\[\frac1{k_{\rm{eff}}}=\frac1{k_1}+\frac1{k_2}\]](/images/math/d/d/7/dd739f2d91c285f8b9f2d0aebfb016c6.png)
![\[\omega=\sqrt{\frac{k_{1}+k_{2}}{m}}\]](/images/math/8/e/e/8ee1d4ae0de770121b420220806b164f.png)
![\[\mu=0,402\]](/images/math/9/f/9/9f987e440f21f70f39079ae0386e4e7c.png)
![\[K = m l \omega^2\]](/images/math/b/c/1/bc196a0738af918a4707795ff1561050.png)
