„Mechanika - Tengerbe lógatott drótkötél” változatai közötti eltérés

A lap 2013. augusztus 29., 11:33-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései) (→‎Feladat) ← Régebbi szerkesztés		A lap jelenlegi, 2015. november 18., 16:06-kori változata (lapforrás) Gombkoto (vitalap | szerkesztései)
11. sor:		11. sor:
	== Megoldás ==		== Megoldás ==
−	<wlatex>A tengerszint alatt $x$ mélységben $l=L-x$ hosszúságú kötéldarab súlya feszíti a kötelet. A felhajtóerő a kötél aljánál ébred, és $F_f=AL\rho_vg$ Az eredő feszítő erő $x$ mélységben tehát $$F(x)=Al\rho g-AL\rho_v g,$$ amely $x=0$-nál maximális $$F(0)=AL(\rho-\rho_v)g,$$ és ott a feszültség $$\sigma=L(\rho-\rho_v)g=0,6\cdot10^9\,\frac{\rm N}{\rm m^2},$$ amely kisebb a szakítószilárdságnál, tehát a kötél nem szakad el.</wlatex>	+	<wlatex>A kötél aljától $x$ távolságra felfelé lévő pontban $x$ hosszúságú kötéldarab súlya feszíti a kötelet. Mivel a felhajtó erő is térfogati erő, hasonlóan oszlik el a kötél mentén, így az eredő feszítő erő $x$ függvényében $$F(x)=\rho Axg-\rho_v Axg,$$ amely $x=0$-nál nulla. $$F(L)=(\rho-\rho_v)ALg,$$ és ott a feszültség $$\sigma(L)=(\rho-\rho_v)Lg=0,6\cdot10^9\,\frac{\rm N}{\rm m^2},$$ amely kisebb a szakítószilárdságnál, tehát a kötél nem szakad el.</wlatex>
	</noinclude>		</noinclude>

---

A lap jelenlegi, 2015. november 18., 16:06-kori változata

[rejt] Navigáció Pt·1·2·3
Kísérleti fizika gyakorlat 1.
Gyakorlatok listája: Deriválás Integrálás Mozgástan Erőtan I. Erőtan II. Munka, energia Pontrendszerek Merev testek I. Merev testek II. Rugalmasság, folyadékok Rezgések I. Rezgések II. Hullámok
Mechanika - Rugalmasság, folyadékok
Feladatok listája: Tengerbe lógatott drótkötél Fémhuzal önsúllyal Rugalmas energia sűrűsége Rezgő merev rúd feszültségállapota Rétegezett folyadékok Vízbe merített farúd Medencefal terhelése Fagolyó vízcsőben Forgó folyadék felszíne Folyadékóra Kifolyás sebessége Lamináris áramlás Jegesmedve jégtáblán
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

1. (5.1.) Egy hajóról a 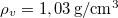sűrűségű tengerbe lógatnak függőlegesen egy 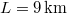hosszú drótkötelet (keresztmetszete 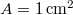, sűrűsége 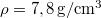, szakítószilárdsága 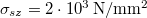). Elszakad-e a kötél?

Megoldás

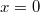A kötél aljától távolságra felfelé lévő pontban hosszúságú kötéldarab súlya feszíti a kötelet. Mivel a felhajtó erő is térfogati erő, hasonlóan oszlik el a kötél mentén, így az eredő feszítő erő függvényében amely -nál nulla. és ott a feszültség amely kisebb a szakítószilárdságnál, tehát a kötél nem szakad el.