„Mechanika - Kocka a vízben” változatai közötti eltérés
A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika gyakorlat 1. Kategória:Szerkesztő:Gombkötő Kategória:Mechanika {{Kísérleti fizika gyakorlat | tárgynév …”) |
|||
| 11. sor: | 11. sor: | ||
== Megoldás == | == Megoldás == | ||
| − | <wlatex> | + | <wlatex>Legyen két kockánk egy víznél kicsit sűrűbb homogén anyagból. Az egyik oldaléle $a$, a másiké pedig $b<a$. A kis kockát a nagyra helyezzük úgy, hogy tökéletesen érintkeznek egy $b^2$ nagyságú négyzetes felületen, azaz közülük kiszorítjuk a vizet, felületeik pedig vízszintesek illetve függőlegesek. Határozd meg az eredő felhajtóerőt a két kockára külön-külön és együttesen felületi integrálással! Hol támad a két kockatérfogatra vonatkozó felhajtóerő rész, és hol támad az eredőjük? Lassú süllyedésük közben szétválnak-e a kockák? Hogyan függ ez $b$-től?</wlatex> |
</noinclude> | </noinclude> | ||
A lap 2015. november 18., 15:29-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- feladat szövege
Megoldás
Legyen két kockánk egy víznél kicsit sűrűbb homogén anyagból. Az egyik oldaléle 
, a másiké pedig 
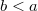. A kis kockát a nagyra helyezzük úgy, hogy tökéletesen érintkeznek egy 
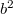nagyságú négyzetes felületen, azaz közülük kiszorítjuk a vizet, felületeik pedig vízszintesek illetve függőlegesek. Határozd meg az eredő felhajtóerőt a két kockára külön-külön és együttesen felületi integrálással! Hol támad a két kockatérfogatra vonatkozó felhajtóerő rész, és hol támad az eredőjük? Lassú süllyedésük közben szétválnak-e a kockák? Hogyan függ ez 
-től?
