Mechanika - Vízbe merített farúd
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2013. június 11., 13:40-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Rugalmasság, folyadékok |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (5.6.) Vékony, egyenletes
 keresztmetszetű,
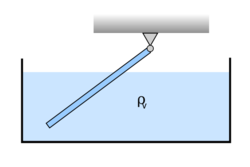
keresztmetszetű,  hosszúságú fa rudat egyik végénél minden irányban elforgatható módon felfüggesztünk, másik végét pedig vízbe merítjük az ábra szerint. Mennyi a rúd vízből kiálló részének
hosszúságú fa rudat egyik végénél minden irányban elforgatható módon felfüggesztünk, másik végét pedig vízbe merítjük az ábra szerint. Mennyi a rúd vízből kiálló részének  hossza, ha a rúd sűrűsége
hossza, ha a rúd sűrűsége 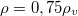 ?
?
Megoldás
A rúd egyensúlyához szükséges a nulla eredő erő és forgatónyomaték. Az előbbihez a csuklópontnál fel lehet venni egy megfelelő kényszererőt, azonban ezt nem kell meghatározni, ha a nyomatéki egyenletet a csuklópontba írjuk fel, kizárólag a súlyerő és a felhajtóerő nyomatékára lesz szükség. Ha a rúd a függőlegessel szöget zár be, a súlyerő nyomatéka
szöget zár be, a súlyerő nyomatéka ![\[M=mg\frac L2\sin{\alpha}=\frac34\rho_vALg\frac L2\sin{\alpha},\]](/images/math/f/3/a/f3a3fc39ec913f2f953e2cb78db19dcb.png)
![\[M_{fel}=m_vg\left(x+\frac{L-x}2\right)\sin{\alpha}=\rho_vA(L-x)g\frac{L+x}2\sin{\alpha}\]](/images/math/0/2/9/0297d05760b5a6eaa1f704d73e28143f.png)
![\[\frac{3L^2}8=\frac{L^2-x^2}2,\]](/images/math/0/c/f/0cf28d43527fda0e2cff48674a963734.png)
![\[x=\frac L2\]](/images/math/c/1/f/c1f6139f4dd53acc2854dab1ae387200.png)